Cho a, b\(\in\)R; \(a+b\ge2\).
Chứng minh ít nhất 1 trong 2 phương trình \(x^2+2ax+b=0\)và \(x^2+2bx+a=0\)có nghiệm.
(Câu hỏi chí mang tính chất thách đố vì đã biết làm, cần cách trình bày tốt nhất )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left|x-1\right|< 3\Leftrightarrow-3< x-1< 3\Leftrightarrow-2< x< 4\)
\(\Rightarrow A=\left(-2;4\right)\)
\(\left|x+2\right|>5\Rightarrow\left[{}\begin{matrix}x+2>5\\x+2< -5\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x>3\\x< -7\end{matrix}\right.\)
\(\Rightarrow B=\left(-\infty;-7\right)\cup\left(3;+\infty\right)\)
\(A\cup B=\left(-\infty;-7\right)\cup\left(-2;+\infty\right)\)
\(A\cap B=\left(3;4\right)\)

\(A\cup B=\left(-1;+\infty\right)\)
\(A\cap B=(2;5]\)

Tham khảo:
Ta có:
Bất phương trình \(1 - 2x \le 0\) có nghiệm là \(x \ge \frac{1}{2}\) hay \(A = [\frac{1}{2};+\infty)\)
Bất phương trình \(x - 2 < 0\) có nghiệm là \(x < 2\) hay \(B = ( - \infty ;2)\)
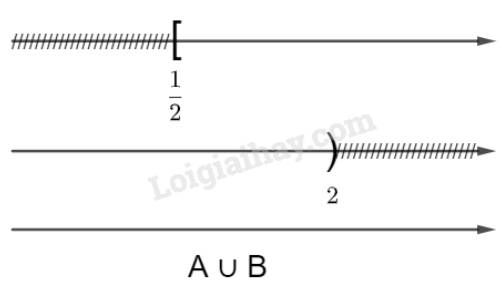
Vậy \(A \cup B = \mathbb R\)
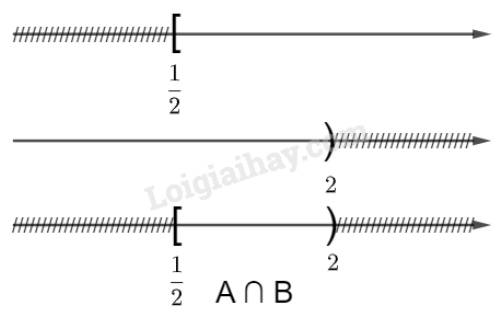
Vậy \(A \cap B = [\frac{1}{2};2)\)

Trước tiên, ta xác định tập hợp B\A: B\A là tập hợp các phần tử thuộc tập B mà không thuộc tập A. Tập A chứa các giá trị x thỏa mãn |mx-3|=mx-3. Điều này có nghĩa là ta cần tìm các giá trị x mà khi thay vào phương trình trên, phương trình vẫn đúng.
Tiếp theo, ta xác định tập hợp B: B là tập hợp các giá trị x thỏa mãn x^2-2x-4=0. Để giải phương trình này, ta có thể sử dụng công thức nghiệm của phương trình bậc 2, hoặc sử dụng định lý Viết.
Giải phương trình x^2-2x-4=0 bằng cách sử dụng công thức nghiệm của phương trình bậc 2, ta có: x = (2 ± √(2^2 - 41(-4))) / (2*1) = (2 ± √(4 + 16)) / 2 = (2 ± √20) / 2 = 1 ± √5
Vậy tập hợp B là B = {1 + √5, 1 - √5}.
Cuối cùng, ta xác định tập hợp B\A: B\A là tập hợp các phần tử thuộc tập B mà không thuộc tập A. Điều này có nghĩa là ta cần loại bỏ các giá trị x thuộc tập A khỏi tập B.
Từ phương trình |mx-3|=mx-3, ta có hai trường hợp để xác định tập A:
Khi mx-3 > 0, ta có mx-3 = mx-3, điều này đúng với mọi giá trị x.Khi mx-3 < 0, ta có -(mx-3) = mx-3, điều này đúng khi mx > 3.Với mọi giá trị x thỏa mãn mx > 3, ta có x thuộc tập A.
Vậy tập hợp B\A = B - A = {1 + √5, 1 - √5} - {x | mx > 3}.
Để tìm m sao cho B\A = B, ta cần tìm giá trị m mà tập hợp B\A bằng tập hợp B. Tức là, ta cần giải phương trình sau: {1 + √5, 1 - √5} - {x | mx > 3} = {1 + √5, 1 - √5}.
Điều này xảy ra khi và chỉ khi tập hợp {x | mx > 3} không chứa bất kỳ giá trị nào từ tập hợp {1 + √5, 1 - √5}. Nghĩa là không có giá trị x thỏa mãn mx > 3 và x thuộc {1 + √5, 1 - √5}.
Vì vậy, để B\A = B, ta cần tìm giá trị m sao cho không có giá trị x thuộc {1 + √5, 1 - √5} thỏa mãn mx > 3.
Tuy nhiên, không có giá trị m nào thỏa mãn yêu cầu trên vì tập hợp {1 + √5, 1 - √5} chứa cả hai giá trị x lớn hơn 3 và nhỏ hơn 3.
Vậy không tồn tại giá trị m để B\A = B.

Lời giải:
\(A\setminus B = \left\{0\right\}\cup (10;+\infty)\)

Phương trình \({x^2} - 5x - 6 = 0\) có hai nghiệm là -1 và 6, nên \(A = \{ - 1;6\} \)
Phương trình \({x^2} = 1\) có hai nghiệm là 1 và -1, nên \(B = \{ - 1;1\} \)
Do đó
\(\begin{array}{l}A \cap B = \{ - 1\} ,\\A \cup B = \{ - 1;1;6\} ,\\A\backslash B = \{ 6\} ,\\B\backslash A = \{ 1\} ,\end{array}\)

Lời giải:
Theo đề thì: \(B\subset A\) nên \(A\cap B = B [-2;1)\)