Xác định dấu của a,b,c trong trường hợp
a) a2b3c6<0; a+b>0; c3-|a|>0
b) |a2+b3c|+5c3<0; (-3a2b)2ac<0; a+b<0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
3
D
16 tháng 2 2020
Vì a,b < 0 suy ra a,b là số nguyên âm = số âm nhân số dương.
Mà a<b suy ra là số nguyên âm và b là số nguyên dương.
Vậy a là số nguyên âm, b là số nguyên dương và a,b khác dấu ( a,b trái dấu )
@ hc tốt !!!!
NT
3
2 tháng 2 2018
Vì a.b<0 nên a hoặc b phải có dấu -
vì a<b nên a có dấu -, b có dấu + thì a<b được
TH
2 tháng 2 2018
Ta có a.b < 0
\(\Rightarrow\hept{\begin{cases}-a;b\\a;-b\end{cases}}\)
Mà a < b nên
\(\Rightarrow-a;b\)
Vậy a mang dấu trừ,b mang dấu cộng
2 tháng 2 2020
\(a.\) \(a.b< 0\)
\(\Leftrightarrow a\) và \(b\) là 2 số khác dấu.
Mà: \(a>b\)
\(\Rightarrow\) \(a\) là số âm và \(b\) là số dương.
2 tháng 2 2020
\(b.\) \(a.b>0\)
\(\Leftrightarrow a\) và \(b\) cùng dấu
Mà: \(a+b< 0\)
\(\Rightarrow a\) và \(b\) là số âm.
VT
15 tháng 5 2018
a) Các điện tích q 1 v à q 2 gây ra tại C các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ:
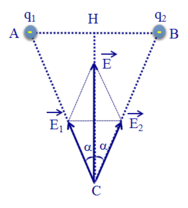
Có độ lớn: E 1 = E 2 = k | q 1 | A C 2 = 9.10 9 .8.10 − 6 0 , 25 2 = 11 , 52 . 10 5 (V/m);
Cường độ điện trường tổng hợp tại C là: E → = E 1 → + E 2 → có phương chiều như hình vẽ, có độ lớn:
E = E 1 . cos α + E 2 cos α = 2 E 1 cos α = 2 E 1 C H A C = 2 . 11 , 52 . 10 5 . 25 2 − 10 2 25 = 21 , 12 . 10 5 ( V / m )
b) Điện tích q 3 đặt tại H gây ra tại C véc tơ cường độ điện trường E ' → sao cho E → + E ' → = 0 → ð E → = - E ' → . Để thoả mãn điều đó thì q 3 < 0 và có độ lớn:
| q 3 | = E . H C 2 k = 11 , 52.10 5 . ( 0 , 25 2 − 0 , 1 2 ) 9.10 9 = 6 , 72 . 10 - 6 .
Vậy q 3 = 6 , 72 . 10 - 6 C.
30 tháng 5 2016
Hướng dẫn giải:
a) A = 3x + 2 + |5x|
=> A = 3x + 2 + 5x khi x ≥ 0
A = 3x + 2 - 5x khi x < 0
Vậy A = 8x + 2 khi x ≥ 0
A = -2x + 2 khi x < 0
b) B = 4x - 2x + 12 khi x ≥ 0
B = -4x -2x + 12 khi x < 0
Vậy B = 2x + 12 khi x ≥ 0
B = -6x khi x < 0
c) Với x > 5 => x - 4 > 1 hay x - 4 dương nên
C = x - 4 - 2x + 12 = -x + 8
Vậy với x > 5 thì C = -x + 8
d) D= 3x + 2 + x+ 5 khi x + 5 ≥ 0
D = 3x + 2 - (x + 5) khi x + 5 < 0
Vậy D = 4x + 7 khi x ≥ -5
D = 2x - 3 khi x < -5
30 tháng 5 2016
Hướng dẫn giải:
a) A = 3x + 2 + |5x|
=> A = 3x + 2 + 5x khi x ≥ 0
A = 3x + 2 - 5x khi x < 0
Vậy A = 8x + 2 khi x ≥ 0
A = -2x + 2 khi x < 0
b) B = 4x - 2x + 12 khi x ≥ 0
B = -4x -2x + 12 khi x < 0
Vậy B = 2x + 12 khi x ≥ 0
B = -6x khi x < 0
c) Với x > 5 => x - 4 > 1 hay x - 4 dương nên
C = x - 4 - 2x + 12 = -x + 8
Vậy với x > 5 thì C = -x + 8
d) D= 3x + 2 + x+ 5 khi x + 5 ≥ 0
D = 3x + 2 - (x + 5) khi x + 5 < 0
Vậy D = 4x + 7 khi x ≥ -5
D = 2x - 3 khi x < -5
1 tháng 8 2017
a) Ta có : A = 3x + 2 + |5x|
+ x ≥ 0 thì A = 3x + 2 + 5x
=> A = 8x + 2
+ x < 0 thì A = 3x + 2 - 5x
=> A = 2 - 2x
BD
14 tháng 8 2017
Ta có : A=3x+2 + |5x|
\(x\ge0\) thì A = 3x+2+5x
=>A=8x+2
x<0 thì A=3x+2-5x
=>A=2-2x
30 tháng 5 2016
a) A = 3x + 2 + |5x|
=> A = 3x + 2 + 5x khi x ≥ 0
A = 3x + 2 - 5x khi x < 0
Vậy A = 8x + 2 khi x ≥ 0
A = -2x + 2 khi x < 0
30 tháng 5 2016
b) B = 4x - 2x + 12 khi x ≥ 0
B = -4x -2x + 12 khi x < 0
Vậy B = 2x + 12 khi x ≥ 0
B = -6x khi x < 0
NT
3
3 tháng 4 2016
Vì a.b<0 nên a,b khác dấu
*)Nếu a dương, b âm
mà |a|=|b|5
nên |a|=|-b|5 hay a=-b5
*)Nếu a âm, b dương
mà |a|=|b|5
nên |-a|=|b|5 hay a=b5(loại)
Vậy dấu của a là dương, còn b là âm
4 tháng 4 2016
vì a*b<0suy ra a,b khác dấu
nếu a dương b âm thì a=-b^5 mà 5 là số lẻ lẽ suy ra -b^5 âm (vô lí)
nếu a âm b dương thì a=b^5 mà b dương nên b dương suy ra bài toán đúng khi a âm ,b dương
vậy dấu của a là - dấu của b là +