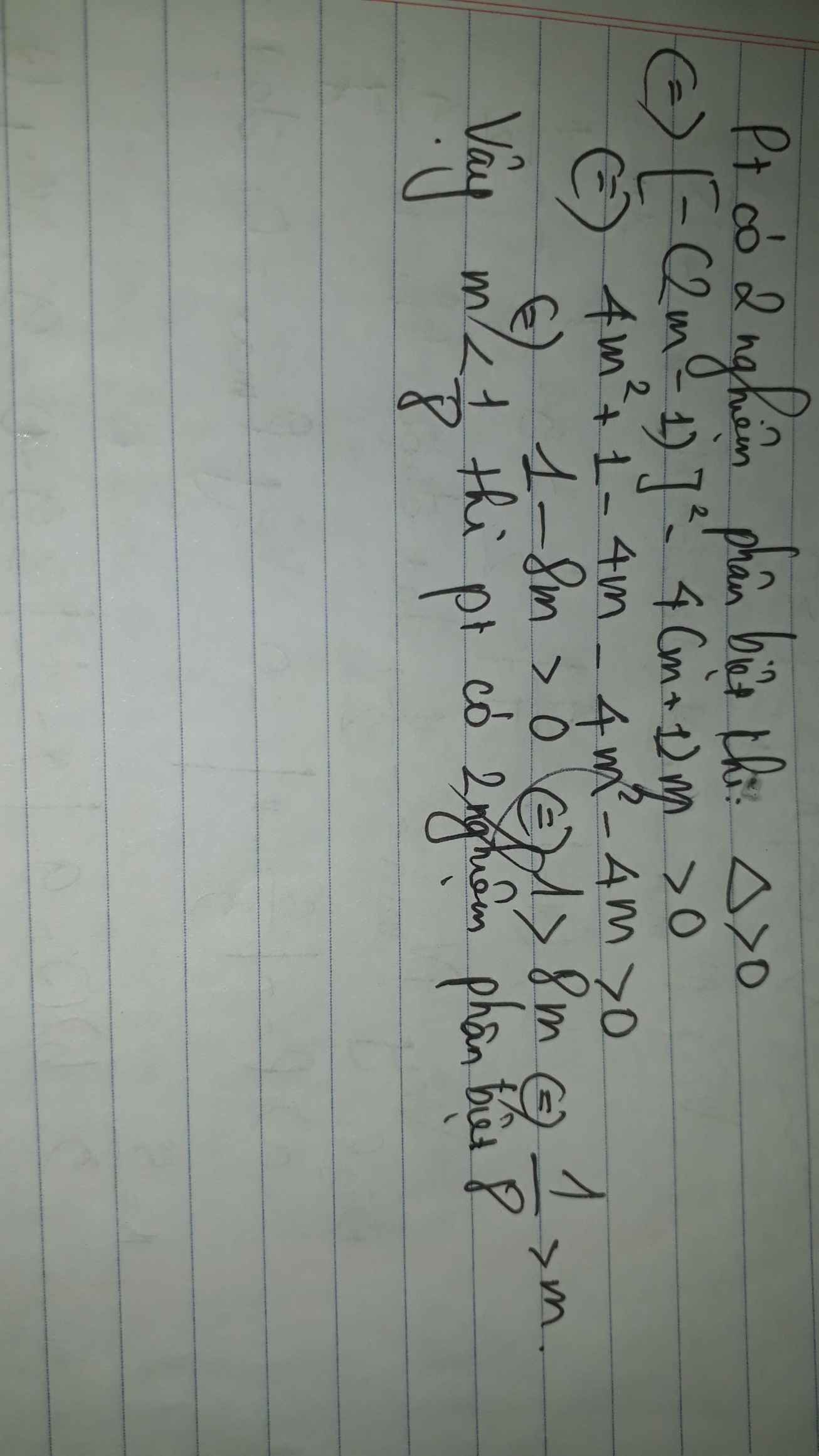Tìm điều kiện của tham số m để phương trình: \(\left(m^2-4\right)x^2+\left(m-2\right)x+3=0\) là pt bậc nhất một ẩn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 7 2021
\(\Delta=\left(2m-1\right)^2-4\cdot\left(m+1\right)\cdot m\)
\(=4m^2-4m+4-4m^2-4m\)
\(=-8m+4\)
Để phương trình có hai nghiệm phân biệt thì
\(\left\{{}\begin{matrix}m+1\ne0\\-8m+4>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ne1\\-8m>-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne1\\m< \dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m< \dfrac{1}{2}\)
18 tháng 7 2021
Ta có: \(\text{Δ}=\left(1-4m\right)^2-4\left(3-2m\right)\left(1-2m\right)\)
\(=16m^2-8m+4-4\left(2m-3\right)\left(2m-1\right)\)
\(=16m^2-8m+4-4\left(4m^2-2m-6m+3\right)\)
\(=16m^2-8m+4-4\left(4m^2-8m+3\right)\)
\(=16m^2-8m+4-16m^2+32m-12\)
\(=24m-8\)
Để phương trình có hai nghiệm phân biệt thì
\(\left\{{}\begin{matrix}3-2m\ne0\\24m-8>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2m\ne3\\24m>8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{3}{2}\\m>\dfrac{1}{3}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 3 2023
\(\Delta'=\left(m-1\right)^2+m^3-\left(m+1\right)^2=m^3-4m\ge0\) \(\Rightarrow\left[{}\begin{matrix}m\ge2\\-2\le m\le0\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-m^3+\left(m+1\right)^2\end{matrix}\right.\)
Do \(x_1+x_2\le4\Rightarrow m-1\le2\Rightarrow m\le3\)
\(\Rightarrow\left[{}\begin{matrix}2\le m\le3\\-2\le m\le0\end{matrix}\right.\)
\(P=x_1^3+x_2^3+3x_1x_2\left(x_1+x_2\right)+8x_1x_2\)
\(=\left(x_1+x_2\right)^3+8x_1x_2\)
\(=8\left(m-1\right)^3+8\left[-m^3+\left(m+1\right)^2\right]\)
\(=8\left(5m-2m^2\right)\)
\(P=8\left(5m-2m^2-2+2\right)=16-8\left(m-2\right)\left(2m-1\right)\le16\)
\(P_{max}=16\) khi \(m=2\)
\(P=8\left(5m-2m^2+18-18\right)=8\left(9-2m\right)\left(m+2\right)-144\ge-144\)
\(P_{min}=-144\) khi \(m=-2\)
TQ
Tìm điều kiện của m để phương trình sau là phương trình bậc nhất một ẩn
\(\left(m^2-4\right)x+k+1=0\)
1
6 tháng 2 2017
(m^2-4)x+k+1=0
*/ ký hiệu k hơi khó hiểu nếu là (y) hiểu là ẩn luôn là (k) lên suy ra k là tham số hay hay ẩn.
Giải theo k luôn:
*-Nếu coi k là ẩn thì : m=+-2
*-Nếu coi k là tham số thì: m khác +-2
4 tháng 3 2023
Để đây làpt bậc nhất 1 ẩn thì m^2-4=0 và m-2<>0
=>m=-2
13 tháng 3 2021
a) Thay m=-2 vào pt:
\(x^2-2.\left(-2+1\right).x-\left(-2+2\right)=0\\ \Leftrightarrow x^2+2x=0\\ \Leftrightarrow x.\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x+2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Với m= -2 => S= {-2;0}
b) Để phương trình trên có 1 nghiệm x1=2:
<=> 22 -2.(m+1).2-(m+2)=0
<=> 4-4m -4 -m-2=0
<=> -5m=2
<=>m=-2/5
c) ĐK của m để pt trên có nghiệm kép:
\(\Delta'=0\\ \Leftrightarrow\left(m+1\right)^2+1.\left(m+2\right)=0\\ \Leftrightarrow m^2+3m+3=0\)
Vô nghiệm.
23 tháng 2 2020
(m-2) x -(m-1) =0
Để PT đã cho là phương trình bậc nhất một ẩn thì
=> m - 2 \(\ne\)0
=> m \(\ne\)2
Vậy m \(\ne\)2 thì (m-2) x - m +1 là phương trình bậc nhất một ẩn.
Câu này thực chất bạn chỉ cần đưa về dạng ax+b =0 rồi lập luận là được. Chúc bạn học tốt.
23 tháng 2 2020
Để phương trình bậc nhất 1 ẩn thì \(m-2\ne0\)
\(\Rightarrow m\ne2\)
Vậy m\(\ne\)2 thì phương trình là phương trình bậc nhất 1 ẩn