Mn ơi, cho e hỏi là tìm số trung bình cộng từ 1 đến 9 thì giải như nào ạ, e dg cần rất gấp, mong mn giúp đỡ ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đường lối ngoại giao của Vua Quang Trung:
- Đối với nhà Thanh: Mềm dẻo nhưng cương quyết bảo vệ từng tấc đất của Tổ quốc.
- Đối với Lê Duy Chỉ ở phía Bắc, Nguyễn Ánh ở phía Nam: kiên quyết tiến quân, tiêu diệt hoàn toàn.
* Ý nghĩa:
- Tránh tình trạng nội chiến, chia cắt đất nước.
- Bảo vệ được toàn vẹn lãnh thổ, độc lập dân tộc, tạo hòa hiếu láng giềng với nhà Thanh.
- Thể hiện sức mạnh của đất nước Đại Việt thời đó.
* Đường lối ngoại giao của Vua Quang Trung:
- Đối với nhà Thanh: Mềm dẻo nhưng cương quyết bảo vệ từng tấc đất của Tổ quốc.
- Đối với Lê Duy Chỉ ở phía Bắc, Nguyễn Ánh ở phía Nam: kiên quyết tiến quân, tiêu diệt hoàn toàn.
* Ý nghĩa:
- Tránh tình trạng nội chiến, chia cắt đất nước.
- Bảo vệ được toàn vẹn lãnh thổ, độc lập dân tộc, tạo hòa hiếu láng giềng với nhà Thanh.
- Thể hiện sức mạnh của đất nước Đại Việt thời đó.



ĐKXĐ: \(x\notin\left\{0;-9\right\}\)
Ta có: \(\dfrac{1}{x+9}-\dfrac{1}{x}=\dfrac{1}{5}+\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{20x}{20x\left(x+9\right)}-\dfrac{20\left(x+9\right)}{20x\left(x+9\right)}=\dfrac{4x\left(x+9\right)+5x\left(x+9\right)}{20x\left(x+9\right)}\)
Suy ra: \(4x^2+36x+5x^2+45x=20x-20x-180\)
\(\Leftrightarrow9x^2+81x+180=0\)
\(\Leftrightarrow x^2+9x+20=0\)
\(\Leftrightarrow x^2+4x+5x+20=0\)
\(\Leftrightarrow x\left(x+4\right)+5\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\left(nhận\right)\\x=-5\left(nhận\right)\end{matrix}\right.\)
Vậy: S={-4;-5}

Bài 5:
Thay x=1 và y=2 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}-m\cdot1+2=-2m\\1+m^2\cdot2=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2m=-m+2\\2m^2=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\-m=2\end{matrix}\right.\)
=>m=-2
Bài 6:
a: ĐKXĐ: x>=1 và y>=-2
\(\left\{{}\begin{matrix}\sqrt{x-1}-3\sqrt{y+2}=2\\2\sqrt{x-1}+5\sqrt{y+2}=15\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2\sqrt{x-1}-6\sqrt{y+2}=4\\2\sqrt{x-1}+5\sqrt{y+2}=15\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-11\sqrt{y+2}=-11\\\sqrt{x-1}-3\sqrt{y+2}=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{y+2}=1\\\sqrt{x-1}=2+3=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y+2=1\\x-1=25\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=26\\y=-1\end{matrix}\right.\left(nhận\right)\)
b: ĐKXĐ: x<>0 và y<>0
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{8}{x}+\dfrac{15}{y}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{8}{x}+\dfrac{8}{y}=\dfrac{8}{12}=\dfrac{2}{3}\\\dfrac{8}{x}+\dfrac{15}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{7}{y}=\dfrac{-1}{3}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=21\\\dfrac{1}{x}=\dfrac{1}{12}-\dfrac{1}{21}=\dfrac{7-4}{84}=\dfrac{3}{84}=\dfrac{1}{28}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=28\\y=21\end{matrix}\right.\left(nhận\right)\)
c: ĐKXĐ: x<>0 và y<>2
\(\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{3}{y-2}=4\\\dfrac{4}{x}-\dfrac{1}{y-2}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{6}{y-2}=8\\\dfrac{4}{x}-\dfrac{1}{y-2}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{y-2}=7\\\dfrac{2}{x}+\dfrac{3}{y-2}=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y-2=1\\\dfrac{2}{x}=4-\dfrac{3}{1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\left(nhận\right)\)
d: ĐKXĐ: x<>-2y và x<>-y/2
\(\left\{{}\begin{matrix}\dfrac{2}{x+2y}+\dfrac{1}{2x+y}=3\\\dfrac{4}{x+2y}-\dfrac{3}{2x+y}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{6}{x+2y}+\dfrac{3}{2x+y}=9\\\dfrac{4}{x+2y}-\dfrac{3}{2x+y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10}{x+2y}=10\\\dfrac{4}{x+2y}-\dfrac{3}{2x+y}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+2y=1\\\dfrac{3}{2x+y}=4-1=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+2y=1\\2x+y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+4y=2\\2x+y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3y=1\\x+2y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{1}{3}\\x=1-\dfrac{2}{3}=\dfrac{1}{3}\end{matrix}\right.\left(nhận\right)\)
e: ĐKXĐ: x>4 và y<>-2
\(\left\{{}\begin{matrix}\dfrac{3}{\sqrt{x-4}}+\dfrac{4}{y+2}=7\\\dfrac{5}{\sqrt{x-4}}-\dfrac{1}{y+2}=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{3}{\sqrt{x-4}}+\dfrac{4}{y+2}=7\\\dfrac{20}{\sqrt{x-4}}-\dfrac{4}{y+2}=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{23}{\sqrt{x-4}}=23\\\dfrac{5}{\sqrt{x-4}}-\dfrac{1}{y+2}=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x-4}=1\\\dfrac{1}{y+2}=5-4=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-4=1\\y+2=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\left(nhận\right)\)
f: ĐKXĐ: x>=-1
\(\left\{{}\begin{matrix}2\left(x+y\right)+\sqrt{x+1}=4\\\left(x+y\right)-\sqrt{x+1}=-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2\left(x+y\right)+\sqrt{x+1}+\left(x+y\right)-\sqrt{x+1}=4-5=-1\\\left(x+y\right)-\sqrt{x+1}=-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3\left(x+y\right)=-1\\\sqrt{x+1}=-\dfrac{1}{3}+5=\dfrac{14}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+y=-\dfrac{1}{3}\\x+1=\dfrac{196}{9}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{187}{9}\\y=-\dfrac{1}{3}-\dfrac{187}{9}=-\dfrac{190}{9}\end{matrix}\right.\left(nhận\right)\)
Nhiều quá em, em chỉ nên đăng những câu nào cảm thấy khó khăn khi giải quyết thôi

Câu 2:
Ta có: \(\sqrt{x^2-4x+4}=x-1\)
\(\Leftrightarrow2-x=x-1\left(x< 2\right)\)
\(\Leftrightarrow-2x=-3\)
hay \(x=\dfrac{3}{2}\left(tm\right)\)

1. Những cây sẵn trong tự nhiên, tự bản thân nó được dùng để trang trí: cây hoa (hoa hồng, hoa cẩm chướng..), cây tùng, cây sanh.
2. Phương pháp sinh sản vô tính: giâm cành bằng cát, ghép, chiết cành, nuôi cấy mô tế bào.
phương pháp sinh sản hữu tính: thụ phấn trong tự nhiên.
3. chọn chậu cây cảnh dựa trên các yếu tố: chất liệu, kích thước,
4. tránh hư hỏng do va đập cơ học
5. Sử dụng axit abxixic để ức chế sinh trưởng.
6. kỹ thuật sản xuất, an toàn thực phẩm, môi trường làm việc đảm bảo, nguồn gốc sản phẩm rõ ràng.
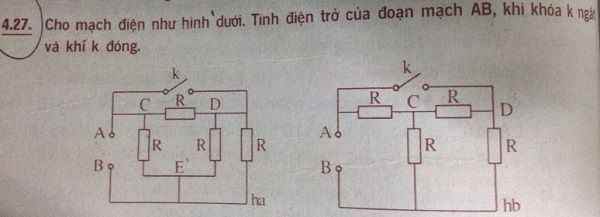 cho e hỏi bai này vs ạ mong mn lm giúp e e đang cần rất gấp
cho e hỏi bai này vs ạ mong mn lm giúp e e đang cần rất gấp




Bạn sẽ tính (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) : 9 = 5
Cảm ơn bn nha