Giúp mình với ạ:') Mik cảm ơn nhiềuuuu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 4 2022
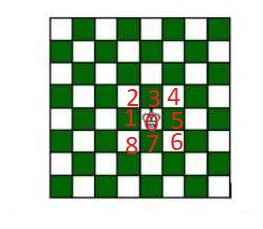
Xung quanh ô quân vua đang đứng có 8 ô, nên ở mỗi một bước, quân vua có 8 cách di chuyển
\(\Rightarrow\) Quân vua có \(8^3\) cách di chuyển 3 bước
Ở bước đầu tiên, quân vua có 3 kiểu đi: sang các ô xanh hoặc sang các ô đỏ
TH1: quân vua sang ô xanh: có 4 cách. Do vai trò các ô như nhau, giả sử quân vua sang ô số 1
Để sau 2 bước nữa quay về ô 0 ban đầu, ở bước tiếp theo nó phải đi vào 1 ô nằm kế ô 0 \(\Rightarrow\) có 4 cách (là các ô 2,3,7,8)
Vậy có 4.4=16 cách
TH2: Quân vua sang ô trắng (có 4 cách) giả sử là ô số 2, vẫn như trên, bước thứ 2 nó phải sang 1 ô nằm kế ô số 0 => có 2 cách
\(\Rightarrow\) 4.2 =8 cách
Vậy quân vua có \(16+8=24\) cách đi thỏa mãn
Xác suất: \(\dfrac{24}{8^3}=...\)
MM
1
16 tháng 12 2021
Bài 6:
a: \(Q=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}{3}\)
\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
28 tháng 6 2023
a: =3/2-2/3:(4/18+3/18)
=3/2-2/3:7/18
=3/2-2/3*18/7
=3/2-12/7
=-3/14
b: =(5/8-1/5)*2-1/4
=5/4-2/5-1/4
=1-2/5=3/5
c: =(3+5/6-1/2):55/12
=10/3*12/55
=8/11
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2022
Bài này xài L'Hopital đi, chứ tách biểu thức chắc đến sáng mai :D
\(\lim\limits_{x\rightarrow1}\dfrac{x^{2020}-2020x+2019}{\left(x-1\right)^2}=\lim\limits_{x\rightarrow1}\dfrac{2020x^{2019}-2020}{2\left(x-1\right)}=\lim\limits_{x\rightarrow1}\dfrac{2019.2020.x^{2018}}{2}=1010.2019\)
Hàm liên tục tại \(x=1\) khi: \(m+1=1010.2019\Rightarrow m=1010.2019-1\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
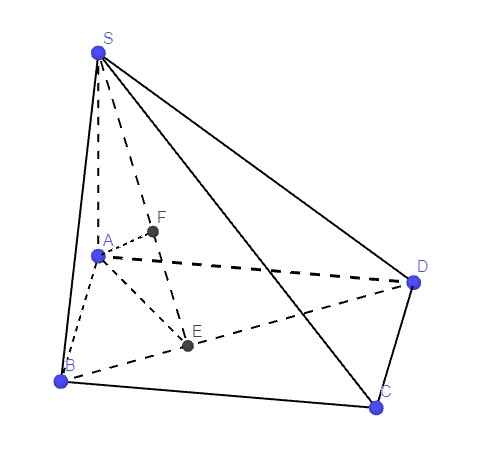
Kẻ \(AE\perp BD\) , \(AF\perp SE\Rightarrow AF\perp\left(SBD\right)\)
Dễ dàng chứng minh \(AD\perp\left(SAB\right)\) ; \(AB\perp\left(SAD\right)\)
Từ đó ta có: \(\alpha=\widehat{FAD}\) ; \(\beta=\widehat{FAB}\) ; \(\gamma=\widehat{FAS}\)
\(\dfrac{1}{AF^2}=\dfrac{1}{SA^2}+\dfrac{1}{AE^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}+\dfrac{1}{AD^2}=\dfrac{2}{a^2}+\dfrac{1}{b^2}=\dfrac{a^2+2b^2}{a^2b^2}\)
\(\Rightarrow AF=\dfrac{ab}{\sqrt{a^2+2b^2}}\)
\(\Rightarrow T=cos\alpha+cos\beta+cos\gamma=\dfrac{AF}{AD}+\dfrac{AF}{AB}+\dfrac{AF}{AS}=\dfrac{ab}{\sqrt{a^2+2b^2}}\left(\dfrac{2}{a}+\dfrac{1}{b}\right)\)
\(\Rightarrow T=\dfrac{\sqrt{3}ab}{\sqrt{\left(1+2\right)\left(a^2+2b^2\right)}}\left(\dfrac{a+2b}{ab}\right)\le\dfrac{\sqrt{3}ab}{a+2b}\left(\dfrac{a+2b}{ab}\right)=\sqrt{3}\)
Dấu "=" xảy ra khi và chỉ khi \(a=b\)
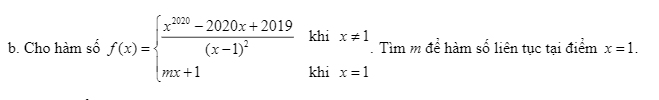
bài đâu
Question-?