Cho nửa đường tròn tâm O, đường kính AB. Trên tia đối của tia AB lấy một điểm M. Vẽ tiếp tuyến MC vs nửa đường tròn. Gọi H là hình chiếu của C trên AB. Giả sử MA = a, MC = 2a, tính AB và CH theo a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

8 tháng 2 2021
( c = 2a )
Tham khảo : https://baitapsgk.com/lop-9/tai-lieu-day-hoc-toan-9/bai-13-trang-95-tai-lieu-day-va-hoc-toan-9-tap-2-cho-nua-duong-tron-o-duong-kinh-ab-tren-tia-doi-cua-tia-ab-lay-mot-diem-m-ve-tiep-tuyen.html

TG
11 tháng 2 2022
b)
Tam giác ABC nội tiếp đường tròn đường kính AB
=> Tam giác ABC vuông tại C
\(\Rightarrow\widehat{ACH}=\widehat{ABC}\) (cùng phụ với góc BAC)
Lại có: Góc M chung
=> ....


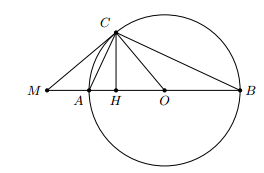
hình hơi chênh lệch, bạn thông cảm vì mình vẽ phần mềm hình olm gà lắm
Xét \(\Delta AMC\)và \(\Delta BCM\)có :
\(\widehat{M}\)( chung ) ; \(\widehat{ACM}=\widehat{CBM}\left(=\frac{1}{2}sđ\widebat{AC}\right)\)
\(\Rightarrow\Delta AMC~\Delta CMB\left(g.g\right)\)
\(\Rightarrow\frac{AM}{MC}=\frac{MC}{MB}\Rightarrow MC^2=MA.MB\)
\(\Rightarrow MB=\frac{MC^2}{MA}=4a\)
Ta có : \(AB=MB-AM=4a-a=3a\)
Xét \(\Delta OCM\)có \(OC\perp CM\) :
\(\Rightarrow S_{OCM}=\frac{1}{2}OC.MC=\frac{1}{2}CH.OM\)
\(\Rightarrow CH=\frac{OC.MC}{OM}=\frac{\frac{AB}{2}.MC}{\frac{AB}{2}+AM}=\frac{6}{5}a\)