Bài 1: Viết các tập hợp sau rôi tìm số phần tử của môi tập hợp đo:
a. Tập hợp A các số tự nhiên x mà 16 : x = 2
b. Tập hợp B các số tự nhiên x mà x +1 < 5
c. Tập hợp C các số tự nhiên x mà x - 4 = x + 4
Bài 2: Viết các tập hợp sau bằng cách liệt kê các phần tử của nó:
a. Tập hợp A các số tự nhiên có hai chữ số, trong đó chữ số hàng chục lớn hơn
chữ số hàng dơn vị là 3.
b. Tập hợp B các số tự nhiên có ba chữ số mà tổng các chữ số bằng 2.
Bài 3: Cho các tập hợp:
A = {1; 2; 5; 4}, B = {3; 4; 5}
Viết các tập họp vừa là tập hợp con của A, vừa là tập hợp con của B.
Bài 4: Cho tập hợp:
A = {1; 2; 3}
a. Viết các tập hợp con của A mà mọi phần tử của nó đều là số lẻ
b. Viết các tập hợp con của A.
* DANG 2: ĐÊM
Bài 1: Trong các số tự nhiên từ 1 đến 200, có bao nhiêu số:
a. Chia hêt cho 2 mà không chia hết cho 3?
b. Chia hết cho ít nhất một trong hai số 2 và 3?
c. Không chia hết cho 2 và không chia hết cho 3?
Bài 2: Trong số 100 học sinh có 75 học sinh thích học Toán, 60 học sinh thích
Văn.
a. Nếu có 5 học sinh không thích cả Toán lần Văn thì có bao nhiều học sinh
thích cả hai môn Văn và Toán?
b. Có nhiều nhất bao nhiêu học sinh thích cả hai môn Văn và Toán?
c Có ít nhất bao nhiêu học sinh không thích cả hai môn Văn và Toán?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: A={4}
A có 1 phần tử
b: B={0;1}
B có 2 phần tử
c: \(C=\varnothing\)
C không có phần tử nào
d: D={0}
D có 1 phần tử
e: E={x|\(x\in N\)}
E có vô số phần tử

Bài 47:
a) \(x+3=4\)
\(\Rightarrow x=4-3=1\)
b) \(8-x=5\)
\(\Rightarrow x=8-5=3\)
c) \(x:2=0\)
\(\Rightarrow x=0\cdot2=0\)
d) \(x+3=4\)
\(\Rightarrow x=4-3=1\)
e) \(5\times x=12\)
\(\Rightarrow x=\dfrac{12}{5}\)
f) \(4\times x=12\)
\(\Rightarrow x=\dfrac{12}{4}=3\)

`@` `\text {Ans}`
`\downarrow`
`46,`
`a)`
tập hợp A các số tự nhiên x mà 8 : x = 2
`8 \div x = 2`
`=> x = 8 \div 2 `
`=> x=4`
Vậy, `x=4`
`=> A = {4}`
`b)`
tập hợp B các số tự nhiên x mà x + 3 < 5
`x+3 < 5`
`=> x \in {0; 1}`
`=> B = {0; 1}`
`c)`
tập hợp C các số tự nhiên x mà x - 2 = x + 2
`x - 2 = x + 2`
`=> x - 2 - x - 2 = 0`
`=> (x - x) - (2 + 2) = 0`
`=> 4 = 0 (\text {vô lí})`
Vậy, `x \in`\(\varnothing\)
`=> C = {`\(\varnothing\)`}`
`d)`
tập hơp D các số tự nhiên x mà x + 0 = x
`x + 0 = x`
`=> x = x (\text {luôn đúng})`
Vậy, `x` có vô số giá trị (với x thuộc R)
`=> D = {x \in RR}`
`47,`
`a)`
`x + 3 =4`
`=> x = 4 - 3`
`=> x=1`
Vậy, `x=1`
`=> A = {1}`
`b)`
`8 - x = 5`
`=> x = 8 - 5`
`=> x= 3`
Vậy, `x=3`
`=> B= {3}`
`c)`
`x \div 2 = 0`
`=> x= 0 \times 2`
`=> x=0`
Vậy, `x=0`
`=> C = {0}`
`d)`
`x + 3 = 4` (giống câu a,)
`e) `
`5` `x = 12`
`=> x = 12 \div 5`
`=> x=2,4`
Vậy, `x = 2,4`
`=> E = {2,4}`
`f)`
`4` `x = 12`
`=> x = 12 \div 4`
`=> x=3`
Vậy, `x=3`
`=> F = {3}`
`53,`
`A = {4; 7}`
`B = {4; 5; a}`
`C = { \text {ốc} }`
`D = { \text {cá; cua; ốc} }.`
`@` `\text {Kaizuu lv u.}`

\(a,\) Giải \(8:x=2\Rightarrow x=4\)
Vậy \(A=\left\{4\right\}\) \(\Rightarrow\) Tập A có 1 phần tử
\(b,\) Giải \(x+3< 5\Rightarrow x< 2\)
Vậy \(B=\left\{x\in N|x< 2\right\}\) hay \(B=\left\{0;1\right\}\)
\(\Rightarrow\) Tập B có 2 phần tử
\(c,\) Giải \(x-2=x+2\Rightarrow x-x=2+2\Rightarrow0=4\) (vô lý)
Vậy \(C=\varnothing\) \(\Rightarrow\) Tập C có không có phần tử nào
\(d,\) Giải \(x+0=x\Rightarrow x-x=0\Rightarrow0=0\) (luôn đúng)
Vậy \(D=\left\{0;1;2;3;4;....\right\}\) \(\Rightarrow\) Tập D có vô số phần tử
a) 8 : x = 2
x = 8 : 2
x = 4
Vậy A = {4}
A có 1 phần tử
b) x + 3 < 5
x < 5 - 3
x < 2
⇒ x = 0 hoặc x = 1
Vậy B = {0; 1}
B có 2 phần tử
c) x - 2 = x + 2
x - x = 2 + 2
0x = 4 (vô lý)
Vậy C = ∅
C không có phần tử nào
d) x + 0 = x (luôn đúng)
Vậy D = ℕ
D có vô số phần tử

a, Ta có 8 : x = 2 ó x = 8 : 2 ó x = 4. Vậy tập hợp A cần tìm là A ={4} .
Số phần tử của tập hợp A là 1 phần tử
b, Ta có x + 3 < 5 ó x < 2, mà x ∈ ¥ nên x = 0 hoặc x = 1
Tập hợp B các số tự nhiên cần tìm là B ={0; 1}.
Số phần tử của tập hợp B là 2 phần tử
c, Ta có x – 2 = x + 2 ó 0.x = 4 ó x = ∅ . Tập hợp C = ∅
Số phần tử của tập hợp C là không có phần tử
d, Ta có x : 2 = x : 4 ó x = 0. Tập hợp D = {0}
Số phần tử của tập hợp D là 1 phần tử.
e, Ta có: x + 0 = x ó x = x (luôn đúng với mọi x ∈ ¥ )
Tập hợp E = {0;1;2;3;….}
Số phần tử của tập hợp E là vô số phần tử.

a. A = {8}. Vậy tập hợp A có 1 phần tử.
b. B = {0;1;2;…}. Vậy tập hợp B có vô số phần tử.
c. C = {5}. Vậy tập hợp C có 1 phần tử.
d. D = ∅ . Vậy tập hợp D không có phần tử nào.
e. E = {0;1;2;…}. Vậy tập hợp E có vô số phần tử.
f. F = ∅ . Vậy tập hợp F không có phần tử nào.
g. G = {0;1;2;3}. Vậy tập hợp G có 4 phần tử

a, x – 9 = 13 => x = 13 + 9 => x = 22
Vậy M = {22} và M có 1 phần tử
b, x + 6 = 34
x = 34 – 6
x = 28
Vậy H = {28} và H có 1 phần tử.
c, x.0 = 0 luôn đúng với mọi x ∈ N
Vậy O = N và O có vô số phần tử
d, a) x.0 = 3 không thỏa mãn vì trong tập hợp các số tự nhiên, số nào nhân với 0 cũng bằng 0
Vậy A = { ∅ } và A có 0 phần tử
e, (x – 2)(x – 5) = 0
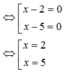
Vậy N = {2;5} và N có 2 phần tử
f, a) x : 0 = 0 không có số tự nhiên nào thỏa mãn vì không thể chia cho 0
Vậy G = { ∅ } và G có 0 phần tử


