Bài 1: Cho tam giác ABC có AB < AC Tia phân giác góc A cắt cạnh BC tại D
Bài 2: Cho tam giác ABC có góc A tù. Trên cạnh AB lấy điểm D
a) So sánh các đoạn thẳng CA,CD và CB
b) Trên cạnh AC lấy điểm E. So sánh DE và BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 7 2023
1:
a: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB<AC
nên BD<CD
b: AB<AC
=>góc B>góc C
góc ADB=góc C+góc CAD
góc ADC=góc B+góc BAD
mà góc C<góc B và góc CAD=góc BAD
nên góc ADB<góc ADC
22 tháng 2 2022
Bài 1:
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB>AC
nên BD>CD
CM
15 tháng 8 2019
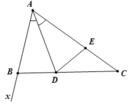
b. Giả sử góc ngoài tại đỉnh B của tam giác ABC là ∠(xBC). Ta có:
∠(xBC) + ∠(ABD) = 180o ⇒ ∠(xBC) = 180o - ∠(ABD) (0.5 điểm)
∠(DEC) + ∠(AED) = 180o ⇒ ∠(DEC) = 180o - ∠(AED) (0.5 điểm)
Mà ∠(ABD) = ∠(AED) ( hai góc tương ứng vì ΔABD = ΔAED)(0.5 điểm)
Từ đó suy ra ∠(xBC) = ∠(DEC) (0.5 điểm)
23 tháng 4 2023
a: \(AC=\sqrt{15^2-9^2}=12\left(cm\right)\)
AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔCBD có
CA vừa là đường cao, vừa là trung tuyến
=>ΔCBD cân tại C
c: Xét ΔCDB có
BE,CA là trung tuyến
BE cắt CA tại I
=>I là trọng tâm
=>DI đi qua trung điểm của BC
