Cho các số x,y>0 thỏa mãn 2x+3y=13. Tìm giá trị nhỏ nhất của Q= x2+y2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
ND
1

12 tháng 12 2020
mk copy trên trang này
https://lazi.vn/edu/exercise/311935/cho-cac-so-thoa-man-2x-3y-13-tim-gia-tri-nho-nhat-cua-q
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
\(2x+3y=13\Rightarrow y=\dfrac{13-2x}{3}\)
\(Q=x^2+\left(\dfrac{13-2x}{3}\right)^2=\dfrac{13}{9}x^2-\dfrac{52}{9}x+\dfrac{169}{9}\)
\(Q=\dfrac{13}{9}\left(x-2\right)^2+13\ge13\)
\(Q_{min}=13\) khi \(\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)

CM
25 tháng 6 2018
Theo đầu bài ta có: log 2x+ log2y=log4(x+y) hay 2 log 2(xy) =log2(x+y)
Suy ra x+y=(xy) 2
Đặt u= x+ y; v= xy ta có điều kiện u2-4v≥0; u>0; v>0 .
Mà ![]()
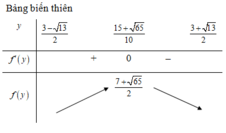
Ta có
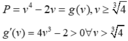
nên minP=
2
4
3
khi 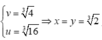
Chọn A.

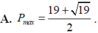
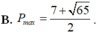
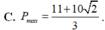
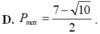
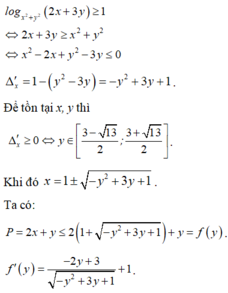
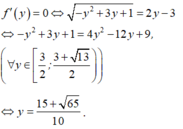
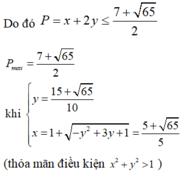

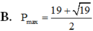
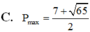
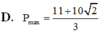



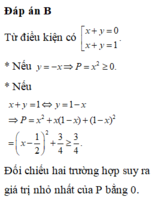
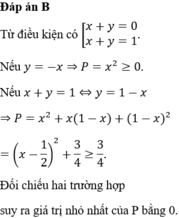
Ta có: 2x + 3y = 13
=> \(13^2=\left(2x+3y\right)^2\le\left(2^2+3^2\right)\left(x^2+y^2\right)\)( theo bunhia)
<=> \(13^2\le13\left(x^2+y^2\right)\)
<=> \(Q=x^2+y^2\ge13\)
Dấu "=" xảy ra <=> \(\frac{x}{2}=\frac{y}{3}=\frac{2x}{4}=\frac{3y}{9}=\frac{2x+3y}{4+9}=\frac{13}{13}=1\)
=> x = 2 và y = 3
Vậy GTNN của Q = 1 tại x = 2 và y = 3.