Cho tam giác ABC cân tại A ;H là trung điểm của BC
Chứng minh tam giác AHB và tam giác AHC
Chứng minh AH vuông BC
Nếu AB bằng 5 Cm AH bằng 3 cm tính BC
Các bạn ơi giúp mk nhé mk đang cần gấp lắm nhớ vẽ hộ mk hình vs nha cảm ơn các bạn nhiều lắm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

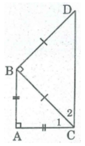
Vì ΔABC vuông cân tại A nên 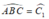
Lại có: 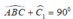 ( tính chất tam giác vuông).
( tính chất tam giác vuông).
Suy ra: ∠ C 1 = 45 0
Vì
∆
BCD vuông cân tại B nên 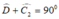
Lại có: ![]() ( tính chất tam giác vuông).
( tính chất tam giác vuông).
Suy ra: ∠ C 2 = 45 0
∠ (ACD) = ∠ C 1 + ∠ C 2 = 45 0 + 45 0 = 90 0
⇒ AC ⊥ CD
Mà AC ⊥ AB (gt)
Suy ra: AB //CD
Vậy tứ giác ABCD là hình thang vuông.

ΔBDC vuông cân tại B
=>góc BCD=góc BDC=45 độ
ΔABC vuông cân tại A
=>góc ABC=góc ACB=45 độ
góc ABC=góc DCB
mà hai góc này ở vị trí so le trong
nên AB//DC
mà AB vuông góc AC
nên DC vuông góc AC
Xét tứ giác ABDC có
AB//DC
góc CAB=90 độ
Do đó: ABDC là hình thang vuông

Vì tam giác ABC vuông cân tại A (gt) nên góc ABC = góc ACB = 90 : 2 = 45 độ
Vì tam giác BCD vuông cân tại B (gt) nên góc BDC = góc BCD = 90 : 2 = 45 độ
Ta có: góc ACB + góc BCD = góc ACD = 45 độ + 45 độ = 90 độ
hay AC vuông góc DC. (1)
Vì tam giác ABC vuông cân tại A (gt) nên AC vuông góc AB (2)
Từ (1) và (2) suy ra DC // AB
Do đó tứ giác ABCD là hình thang.
ai giải bải này cko mik với ạ mik cảm ơn
một thửa ruộng hình chữ nhật có chiều dài 54m, chiếu rộng bằng 2/3 chiều dài người ta cấy lúa trên thửa ruộng đó trung bình 100m vuông thu được 70kg thóc .Hỏi cả thửa ruộng thu được bao nhiêu tạ thóc
a) Vì \(\Delta ABC\)là tam giác cân tại A
=> \(AB=AC\)và \(\widehat{B}=\widehat{C}\)
CM \(\Delta AHB=\Delta AHC\)
Xét \(\Delta AHB\)và \(\Delta AHC\)có :
\(AB=AC\left(cmt\right)\)
\(\widehat{B}=\widehat{C}\left(cmt\right)\)
\(HB=HC\)( vì M là trung điểm của BC )
=> \(\Delta AHB=\Delta AHC\left(c.g.c\right)\)
b) CM \(AH\perp BC\)
Vì \(\Delta AHB=\Delta AHC\)
=> \(\widehat{H_1}=\widehat{H_2}\)( hai góc tương ứng ) ( chỗ này mình vẽ thiếu, bạn tự bổ sung )
mà \(\widehat{H_1}+\widehat{H_2}=180^0\)( kề bù )
=> \(\widehat{H}_1=\widehat{H_2}=\frac{180^0}{2}=90^0\)
=> \(AH\perp BC\)( đpcm )
d) Nếu AB = 5cm , AH = 3cm . Tính BC
Vì \(\widehat{H_1}=90^0\)=> \(\Delta AHB\)là tam giác vuông
=> \(AB^2=AH^2+BC^2\)( Đ/lí Pytago )
Thay AB = 5cm, AH = 3cm ta có
\(5^2=3^2+BC^2\)
\(25=9+BC^2\)
=> \(BC^2=16\)
mà \(\sqrt{16}=4\)=> BC = 4cm