Thí nghiệm: Làm bay hơi 60 gam nước từ dung dịch NaOH có nồng độ 15% được dung dịch mới có nồng độ 18%.
a. Hãy xác định khối lượng dung dịch NaOH ban đầu.
b. Cho m gam natri vào dung dịch thu được trong thí nghiệm trên được dung dịch có nồng độ 20,37%. Tính m.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 8 2019
Gọi x là khối lượng dung dịch ban đầu thì khối lượng dung dịch sau khi làm bay hơi: x – 60.
Khối lượng chất tan trong dung dịch ban đầu:
m ct = ( C % . m dd ) / ( 100 % ) = ( 15 % . x ) / ( 100 % ) = 0 , 15 x
Khối lượng chất tan trong dung dịch sau khi làm bay hơi:
m ct = ( C % . m dd ) / ( 100 % ) = ( 18 % ( x - 60 ) ) / ( 100 % ) = 0 , 18 ( x – 60 )
Mà khối lượng chất tan trước và sau khi bay hơi không đổi (vì chỉ làm bay hơi nước) nên ta có:
0,15x = 0,18(x – 60) → x = 360 gam.
12 tháng 5 2016
Đặt khối lượng dung dịch ban đầu là gam
Vậy khối lượng dung dịch sau khi làm bay hơi là: (m - 60) gam
Khối lượng chất tan có trong dung dịch trước và sau khi làm bay hơi là không đổi, ta có:
mct = =
⇔ 15 . m = 18(m - 60)
⇔ 15m = 18m - 1080
⇔ 3m = 1080
⇔ m = 360 gam
Vậy khối lượng dung dịch ban đầu là 360 gam
1 tháng 6 2017
Gọi m là khối lượng dung dịch ban đầu
Khối lượng dung dịch sau khi làm bay hơi nước bằng (m-60)g.
Khối lượng chất tan trước và sau là không đổi. Ta có:
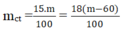
⇔ 15.m = 18(m – 60)
⇔ 15m = 18m – 1080
⇔ 3m = 1080 m = 360 (g)
Vậy khối lượng dung dịch trước khi bay hơi là 360 gam.
6 tháng 7 2021
Gọi khối lượng chất tan là a (gam)
Gọi khối lượng nước là b (gam)
Ta lập được hệ phương trình: \(\left\{{}\begin{matrix}\dfrac{a}{a+b}=0,15\\\dfrac{a}{a+b-60}=0,18\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=54\\b=306\end{matrix}\right.\)
\(\Rightarrow m_{dd\left(ban.đầu\right)}=54+306=360\left(g\right)\)
24 tháng 12 2021
Gọi mH2O(bay hơi) = (g)
\(m_{Fe\left(NO_3\right)_3}=\dfrac{500.10}{100}=50\left(g\right)\)
=> \(C\%\left(ddsaukhibayhoi\right)=\dfrac{50}{500-a}.100\%=25\%\)
=> a = 300(g)
9 tháng 2 2021
Câu 1 :
Ta có : \(20\%=\dfrac{m_{ct}}{m_{dd}}.100\%\left(I\right)\)
Mà : \(25\%=\dfrac{m_{ct}}{m_{dd}-75}.100\%\left(II\right)\)
- Giair hệ phương trình ( I ) và ( II ) ta được : \(m_{dd}=375\left(g\right)\)
