cho tam giác ABC vuông tại A có AB=6cm AC=8cm. tia phân giác góc B cắt AC tại D.tính độ dài AD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


11:
\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos60=\dfrac{2\cdot6\cdot12}{6+12}\cdot\dfrac{1}{2}=4\left(cm\right)\)
12:
\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos60=\dfrac{2\cdot3\cdot6}{3+6}\cdot\dfrac{1}{2}=\dfrac{3\cdot6}{3+6}=\dfrac{18}{9}=2\left(cm\right)\)

a) Áp dụng định lí Py-ta-go vào ΔABC vuông tại A ta có:
\(BC^{ }=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC có BD là p/g \(\widehat{ABC}\),theo t/c ta có:
\(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Rightarrow\dfrac{DC}{BC}=\dfrac{AD}{AB}hay\dfrac{DC}{10}=\dfrac{AD}{6}\)
Theo tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{DC}{10}=\dfrac{AD}{6}=\dfrac{DC+AD}{10+6}=\dfrac{AC}{16}=\dfrac{8}{16}=\dfrac{1}{2}\)
=>\(\left\{{}\begin{matrix}DC=10.\dfrac{1}{2}=5\left(cm\right)\\AD=6.\dfrac{1}{2}=3\left(cm\right)\end{matrix}\right.\)
b) Ta có: \(\widehat{ABD}+\widehat{BDA}=\widehat{BAD}=90^o\)
\(\widehat{DBH}+\widehat{BIH}=\widehat{BHI}=90^o\)
Mà \(\widehat{ABD}=\widehat{DBH}\)(DB là p/g \(\widehat{ABC}\)) ⇒\(\widehat{BDA}=\widehat{BIH}\)
Lại có \(\widehat{AID}=\widehat{BIH}\)( 2 góc đối đỉnh)
⇒\(\widehat{BDA}=\widehat{AID}\)
⇒ΔAID cân tại A
c) Xét ΔABD và ΔHBI có:
\(\widehat{BAD}=\widehat{BHI}=90^o\left(gt\right)\)
\(\widehat{ABD}=\widehat{IBH}\)(BD là p/g \(\widehat{ABC}\))
⇒ΔABD ~ ΔHBI(g-g)
⇒\(\dfrac{AD}{IH}=\dfrac{BD}{BI}\)⇒\(\dfrac{AD}{BD}=\dfrac{IH}{BI}\)
Mà AD=AI(ΔAID cân tại A)⇒\(\dfrac{AI}{BD}=\dfrac{IH}{BI}\Rightarrow AI.BI=BD.IH\left(đpcm\right)\)

Tam giác vuông BAC có ∠A = 90o
Áp dụng định lí Pitago, ta có:
BC2 = AB2 + AC2
= 62 + 82 = 36 + 64 = 100
⇒ BC = 10 (cm)
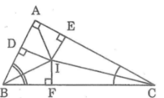
Kẻ IF ⊥ BC
Xét hai tam giác vuông IDB và IFB, ta có:
∠(IDB) = ∠(IFB) = 90o
∠(DBI) = ∠(FBI) (gt)
cạnh huyền BI chung
Suy ra: ΔIDB = ΔIFB (cạnh huyền, góc nhọn)
Suy ra: DB = FB (hai cạnh tương ứng) (4)
Xét hai tam giác vuông IEC và IFC, ta có:
∠(IEC) = ∠(IFC) = 90o
∠(ECI) = ∠(FCI) (gt)
cạnh huyền CI chung
Suy ra: ΔIEC = ΔIFC (cạnh huyền, góc nhọn)
Suy ra: CE = CF (hai cạnh tương ứng) (5)
Mà: AD + AE = AB - DB + AC - CE
Suy ra: AD + AE = AB + AC - (DB + CE) (6)
Từ (4), (5) và (6) suy ra: AD + AE = AB + AC - (FB + FC)
= AB + AC - BC = 6 + 8 - 10 = 4 (cm)
Mà AD = AE (chứng minh trên)
Nên AD = AE = 4 : 2 = 2(cm).

a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC∼ΔHBA(g-g)
Suy ra: \(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=BC\cdot BH\)(đpcm)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Ta có: \(AB^2=BC\cdot BH\)(cmt)
nên \(BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=\dfrac{36}{10}=3.6\left(cm\right)\)
Vậy: BH=3,6cm

Xét ΔABC vuông ở A, theo định lý Pi-ta-go ta được :
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Ta có : AD là phân giác \(\widehat{BAC}\)
\(\Rightarrow\dfrac{BD}{DC}=\dfrac{AB}{AC}\)
hay \(\dfrac{BD}{DC}=\dfrac{6}{8}\)
\(\Rightarrow\dfrac{BD}{6}=\dfrac{DC}{8}=\dfrac{BD+DC}{6+8}=\dfrac{10}{14}=\dfrac{5}{7}\)
\(\Rightarrow BD=\dfrac{5}{7}.6=\dfrac{30}{7}\left(cm\right)\)
\(\Rightarrow DC=\dfrac{5}{7}.8=\dfrac{40}{7}\left(cm\right)\)
Hình bạn tự kẻ nhé!
Xét tam giác ABC vuông tại A có:
AB2 + AC2 = BC2 ( định lý Pytago )
=> 62 + 82 = BC2
<=> 36 + 64 = BC2
<=> 100 = BC2
<=> BC = 10 (cm) ( vì BC > 0 )
Xét tam giác ABC có: BD là đường pg của tam giác ABC
=> DA / DC = AB / BC
=> DA / ( DA + DC ) = AB/ ( BC + AB )
<=> DA / AC = 3/8
<=> AD / 8 = 3/8
<=> AD = 3 (cm)
Vậy AD = 3 cm.

a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
b: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
DO đó: ΔBAD=ΔBED
Suy ra: BA=BE
hay ΔBAE cân tại B

a/ \(BD\) là đường phân giác \(\widehat{BAC}\)
\(\to\dfrac{DA}{DC}=\dfrac{BA}{BC}\) hay \(\dfrac{DA}{DC}=\dfrac{6}{10}=\dfrac{3}{5}\)
\(\to\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{AC}{8}=\dfrac{8}{8}=1\)
\(\to\begin{cases}DA=3\\DC=5\end{cases}\)
b/ \(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.AH.BC\)
\(\to AB.AC=AH.BC\)
\(\to \dfrac{AB.AC}{BC}=AH=\dfrac{6.8}{10}=3,2(cm)\)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
Vậy: AH=4,8cm

Hình bạn tự kẻ nhé!
Xét tam giác ABC vuông tại A có:
AB2 + AC2 = BC2 ( định lý Pytago )
=> 62 + 82 = BC2
<=> 36 + 64 = BC2
<=> 100 = BC2
<=> BC = 10 (cm) ( vì BC > 0 )
Xét tam giác ABC có: BD là đường pg của tam giác ABC
=> DA / DC = AB / BC
=> DA / ( DA + DC ) = AB/ ( BC + AB )
<=> DA / AC = 3/8
<=> AD / 8 = 3/8
<=> AD = 3 (cm)
Vậy AD = 3 cm.