Cho tứ giác ABCD có AD=BC và AB

LT

Linh Tâm

5 tháng 4 2020

Cho tứ giác ABCD có AD=BC và AB<CD. Trung điểm của cạnh AB và CD lần lượt là M và N. Trung điểm của các đường chéo BD và AC lần lượt là P và Q. a) Chứng minh tứ giác MPNQ là hình thoi b) Kéo dài hai cạnh DA và CB cắt nhau tại G, kẻ tia phân giác Gx của góc AGB. Chứng minh Gx//MN. c) Tứ giác ABCD cần thêm điều kiện gì để MPNQ là hình vuông? Chứng...

Đọc tiếp

#Toán lớp 8

1

IH

Inosuke Hashibira

5 tháng 4 2020

Bạn có thể vô link này tham khảo tuy là không được đầy đủ. Nếu có tg mik làm lại cho.

Câu hỏi của nguyen thanh lan - Toán lớp 8 - Học toán với OnlineMath

Đúng(0)

TB

Tran Bao Uyen Nhi

17 tháng 7 2018 - olm

1/Cho tứ giác ABCD có AB//CD,AD//BC.Chứng minh AD=BC,AB=CD.

2/Cho tứ giác ABCD có AB//CD,AB=CD.Chứng minh AD//BC và AD=BC

#Toán lớp 7

1

BZ

Bronya Zaychik

26 tháng 11 2022

1/nối AC

Do AB//CD=>BAC=ACD(so le trong)

Do AD//BC=>ACB=DAC(so le trong)

Xét ∆ABC và ∆ACD

ACB=DAC(chứng minh trên)

BAC=DAC(chứng minh trên)

AC chung

Vậy ∆ABC=∆CDA(g.c.g)=>AB=DC(cặp cạnh tương ứng)

AD=BC(cặp cạnh tương ứng)

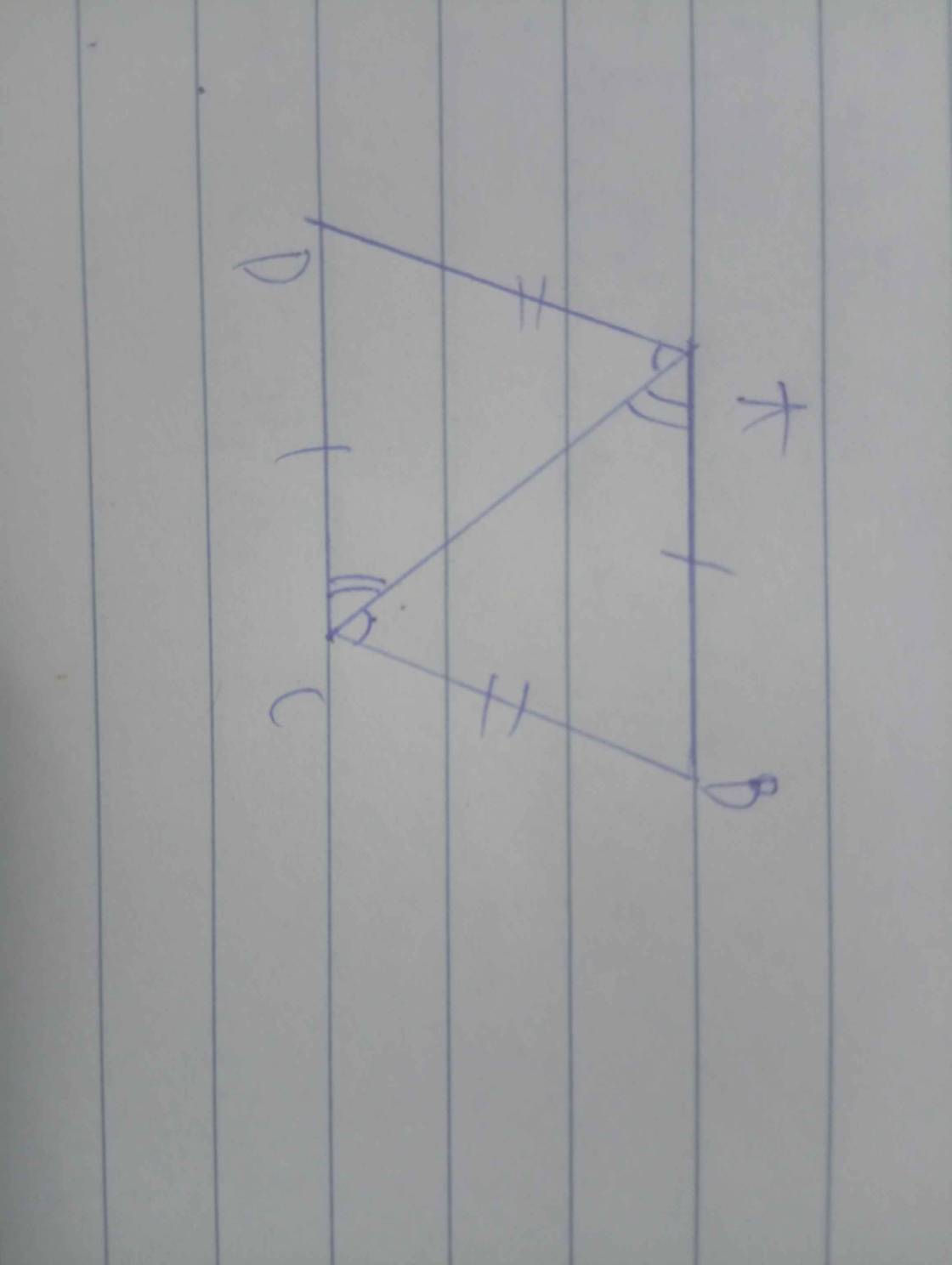
loading...

Đúng(0)

BD

Ba đứa làm CTV

7 tháng 9 2017 - olm

cho tứ giác ABCD có AB // CD và AB = CD . C/m : AD = BC và AD // BC

#Toán lớp 7

3

K

KODOSHINICHI

7 tháng 9 2017

Chứng minh rằng AK=KC,BI=ID
vì FE là đường trung bình hình thang nên FE//AB//CD
E, F là trung điểm của AD và BC nên AK=KC
BI=ID
( trong tam giác đường thẳng qua trung điểm của 1 cạnh, // với cạnh thứ 2 thì qua trung điểm cạnh thứ 3)

Đúng(0)

F

๖Fly༉Donutღღ

7 tháng 9 2017

Xét t/g ABC và t/g CDA có :

AC cạnh chung

AB = CD ( gt )

\(\widehat{A1}=\widehat{C1}\)( slt , AB // CD )

\(\Rightarrow\)t/g ABC = t/g CDA ( c-g-c )

\(\Rightarrow\)BC = AD

\(\widehat{A2}=\widehat{C2}\) và 2 góc này ở vị trí slt

\(\Rightarrow\)BC // AD

Đúng(0)

G

god

8 tháng 11 2021

Câu 17:. Chọn câu đúng:A. Tứ giác ABCD là hình chữ nhật khi có và . B. Tứ giác ABCD là hình chữ nhật khi có và . C. Tứ giác ABCD là hình chữ nhật khi có AB=CD; AD=BC; AC=BD. D. Tứ giác ABCD là hình chữ nhật khi có AB=CD; AB=BC và...

Đọc tiếp

#Toán lớp 8

2

BS

BuBu siêu moe 방탄소년단

8 tháng 11 2021

C

Đúng(0)

NL

Nguyễn Lê Phước Thịnh

8 tháng 11 2021

Chọn C

Đúng(0)

P

pansak9

6 tháng 11 2021

Cho tứ giác ABCD thỏa mãn AB = CD, AD = BC. Chứng minh rằng:
a, △ABC = △CDA
b, AB // CD và AD // BC
~Có vẽ hình~

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

6 tháng 11 2021

b: Xét tứ giác ABCD có

AB=CD

AD=BC

Do đó: ABCD là hình bình hành

Suy ra: AB//CD;AD//BC

Đúng(0)

US

Uchiha Sasuke

13 tháng 7 2017 - olm

Cho tứ giác ABCD có AB song song với CD và AB = CD

C/m : AD = BC và AD song song với BC

#Toán lớp 8

1

NH

Ngô Hải Đăng

17 tháng 9 2020

\(\text{AB song song với CD và AB=CD}\Rightarrow ABCD\text{ là hình bình hành}\)

\(\Rightarrow AD\text{//}BC\text{ và }AD=BC\)

Đúng(0)

PG

Phan Gia Bảo

9 tháng 12 2021

Cho tứ giác ABCD, có AB // CD, AD // với BC. Chứng minh AB=CD, AD=BC

#Toán lớp 8

2

NL

Nguyễn Lê Phước Thịnh

9 tháng 12 2021

Xét tứ giác ABCD có

AB//CD

AD//BC

DO đó: ABCD là hình bình hành

Suy ra: AB=CD; AD=BC

Đúng(1)

GB

Good boy

9 tháng 12 2021

Xét tứ giác ABCD có:

AD//BC

AB//CD

Suy ra: Tứ giác ABCD là hình bình hành vì có 2 cặp cạnh song song

Suy ra: AB=CD; AD=BC

Đúng(1)

YN

yến nguyễn

10 tháng 7 2018 - olm

cho tứ giác abcd có ab//cd, ad//bc cm ab = cd , ad-= bc

#Toán lớp 7

0

HT

Hoàng Tiến Đạt

29 tháng 11 2021 - olm

Cho tứ giác ABCD có AB=CD;AD=BC
Chứng minh rằng:
A: tam giác ABC=tam giác CDA
B:AB//CD VÀ AD//BC

#Toán lớp 7

0

NQ

Nguyễn Quỳnh Trang

3 tháng 4 2023

Cho tứ giác ABCD có diện tích bằng 60 cm2 . Kéo dài các cạnh AB, BC, CD và DA sao cho BM = AB, CN= BC , DP= CD , AQ = AD . Tính diện tích tứ giác MNPQ.

#Toán lớp 5

1

NL

Nguyễn Lê Phước Thịnh

3 tháng 4 2023

AB=BM

nên \(S_{QAB}=S_{QBM}\)

DA=AQ

=>\(S_{BDA}=S_{BAQ}\)

=>\(S_{QAM}=2\cdot S_{ABD}\)

Tương tự, ta được: \(S_{MBN}=2\cdot S_{ABC};S_{NCP}=2\cdot S_{BCD};S_{PDQ}=2\cdot S_{ADC}\)

=>\(S_{MNPQ}=5\cdot S_{ABCD}=300\left(cm^2\right)\)

Đúng(1)

NN

Nguyễn Ngọc Trung

22 tháng 7 2017 - olm

Cho tứ giác ABCD có AB không song song với CD, BC < AD. Gọi E, F lần lượt là trung điểm của đường chéo AC và BD thỏa mãn EF= AD- BC \ 2

CMR : tứ giác ABCD là hình thang

#Toán lớp 8

3

TT

tuan tran

14 tháng 9 2017

Bạn ơi có đáp án câu này không mình xin với. Mình cũng đang học

Đúng(0)

IL

i love hattori

15 tháng 9 2017

Mk ko biết

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP