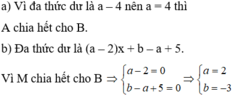Tìm nghiệm của đa thức A(x)=x5-x4-7x3+x2+6x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`@` `\text {Ans}`
`\downarrow`
`a)`
Thu gọn:
`P(x)=`\(5x^4 + 3x^2 - 3x^5 + 2x - x^2 - 4 +2x^5\)
`= (-3x^5 + 2x^5) + 5x^4 + (3x^2 - x^2) + 2x - 4`
`= -x^5 + 5x^4 + 2x^2 + 2x - 4`
`Q(x) =`\(x^5 - 4x^4 + 7x - 2 + x^2 - x^3 + 3x^4 - 2x^2\)
`= x^5 + (-4x^4 + 3x^4) - x^3 + (x^2 - 2x^2) + 7x - 2`
`= x^5 - x^4 - x^3 - x^2 + 7x - 2`
`@` Tổng:
`P(x)+Q(x)=`\((-x^5 + 5x^4 + 2x^2 + 2x - 4) + (x^5 - x^4 - x^3 - x^2 + 7x - 2)\)
`= -x^5 + 5x^4 + 2x^2 + 2x - 4 + x^5 - x^4 - x^3 - x^2 + 7x - 2`
`= (-x^5 + x^5) - x^3 + (5x^4 - x^4) + (2x^2 - x^2) + (2x + 7x) + (-4-2)`
`= 4x^4 - x^3 + x^2 + 9x - 6`
`@` Hiệu:
`P(x) - Q(x) =`\((-x^5 + 5x^4 + 2x^2 + 2x - 4) - (x^5 - x^4 - x^3 - x^2 + 7x - 2)\)
`= -x^5 + 5x^4 + 2x^2 + 2x - 4 - x^5 + x^4 + x^3 + x^2 - 7x + 2`
`= (-x^5 - x^5) + (5x^4 + x^4) + x^3 + (2x^2 + x^2) + (2x - 7x) + (-4+2)`
`= -2x^5 + 6x^4 + x^3 + 3x^2 - 5x - 2`
`b)`
`@` Thu gọn:
\(H (x) = ( 3x^5 - 2x^3 + 8x + 9) - ( 3x^5 - x^4 + 1 - x^2 + 7x)\)
`= 3x^5 - 2x^3 + 8x + 9 - 3x^5 + x^4 - 1 + x^2 - 7x`
`= (3x^5 - 3x^5) + x^4 - 2x^3 - x^2 + (8x + 7x) + (9+1)`
`= x^4 - 2x^3 - x^2 + 15x + 10`
\(R( x) = x^4 + 7x^3 - 4 - 4x ( x^2 + 1) + 6x\)
`= x^4 + 7x^3 - 4 - 4x^3 - 4x + 6x`
`= x^4 + (7x^3 - 4x^3) + (-4x + 6x) - 4`
`= x^4 + 3x^3 + 2x - 4`
`@` Tổng:
`H(x)+R(x)=` \((x^4 - 2x^3 - x^2 + 15x + 10)+(x^4 + 3x^3 + 2x - 4)\)
`= x^4 - 2x^3 - x^2 + 15x + 10+x^4 + 3x^3 + 2x - 4`
`= (x^4 + x^4) + (-2x^3 + 3x^3) - x^2 + (15x + 2x) + (10-4)`
`= 2x^4 + x^3 - x^2 + 17x + 6`
`@` Hiệu:
`H(x) - R(x) =`\((x^4 - 2x^3 - x^2 + 15x + 10)-(x^4 + 3x^3 + 2x - 4)\)
`=x^4 - 2x^3 - x^2 + 15x + 10-x^4 - 3x^3 - 2x + 4`
`= (x^4 - x^4) + (-2x^3 - 3x^3) - x^2 + (15x - 2x) + (10+4)`
`= -5x^3 - x^2 + 13x + 14`
`@` `\text {# Kaizuu lv u.}`

Ta thấy \(B=\left(x-1\right)\left(x-5\right)\) nên để đa thức A chia hết cho đa thức B thì \(A=\left(x-1\right)\left(x-5\right).C\) với \(C\) là một đa thức bậc 2 hệ số nguyên theo \(x\).
Điều này tương đương với việc \(A\) có 2 nghiệm là \(x=1,x=5\). Do đó \(A\left(1\right)=0\) \(\Leftrightarrow1^4-7.1^3+10.1^2+\left(a-1\right)+b-a=0\) \(\Leftrightarrow b=-3\)
Ta viết lại \(A=x^4-7x^3+10x^2+\left(a-1\right)x-3-a\). Ta có \(A\left(5\right)=0\) \(\Leftrightarrow5^4-7.5^3+10.5^2+\left(a-1\right).5-3-a=0\) \(\Leftrightarrow4a-8=0\) \(\Leftrightarrow a=2\).
Vậy để đa thức A chia hết cho đa thức B thì \(a=2,b=-3\).
A:B=x2-x+11 dư (a+70)x+b-a-55
Để A chia hết cho B thì
(a+70)x+b-a-55=0
b-a-55=0 (a khác -70) tại x=0
Vậy b-a=55 thỏa đề bài

c. Thay x = -1 vào A(x) và B(x) ta có:
A(-1) = 0, B(-1) = 2
Vậy x = -1 là nghiệm của A(x) nhưng không là nghiệm của B(x) (1 điểm)

a. Ta có: A(x) = x5 + x2 + 5x + 6 - x5 - 3x - 5
= x2 + 2x + 1 (0.5 điểm)
B(x) = x4 + 2x2 - 3x - 3 - x4 - x2 + 3x + 4 = x2 + 1 (0.5 điểm)


b. Ta có:
A(x) + B(x) = x2 + 2x + 1 + x2 + 1 = 2x2 + 2x + 2 (0.5 điểm)
A(x) - B(x) = x2 + 2x + 1 - (x2 + 1) = 2x (0.5 điểm)