Trong Oxy, cho tam giác ABC có A (1; 4), B (-4; 0), C (3; -2). Gọi G là trọng tâm của tam giác ABC. Viết phương trình đường thẳng đi qua G và song song với trục tung.
MONG MỌI NGƯỜI GIÚP ĐỠ CHO MÌNH! CẢM ƠN RẤT NHIỀU!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 8 2018
Chọn B.
*) AH là đường cao của tam giác ABC.
*) Lập phương trình cạnh BC
B(1;-1), C(5;2)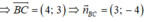 
(BC):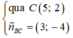 
⇒ 3.(x - 5) - 4.(y - 2) = 0 ⇔ 3x - 15 - 4y + 8 = 0 ⇔ 3x - 4y - 7 = 0
Ta có:
HP
23 tháng 1 2021
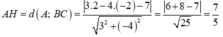
Giả sử trực tâm của tam giác ABC có tọa độ \(H\left(x;y\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{BC}=\left(6;-2\right)\\\overrightarrow{AH}=\left(x-1;y\right)\end{matrix}\right.\Rightarrow\overrightarrow{BC}\perp\overrightarrow{AH}\Leftrightarrow\overrightarrow{AH}.\overrightarrow{BC}=0\)
\(\Leftrightarrow6\left(x-1\right)-2y=0\)
\(\Leftrightarrow3x-y=3\left(1\right)\)
Lại có:
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-2;1\right)\\\overrightarrow{CH}=\left(x-5;y+1\right)\end{matrix}\right.\Rightarrow\overrightarrow{AB}\perp\overrightarrow{CH}\Leftrightarrow\overrightarrow{CH}.\overrightarrow{AB}=0\)
\(\Leftrightarrow-2\left(x-5\right)+y+1=0\)
\(\Leftrightarrow-2x+y=-11\left(2\right)\)
\(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}x=-8\\y=-27\end{matrix}\right.\Rightarrow H\left(-8;-27\right)\)
CM
4 tháng 1 2017
A B → = 3 ; 12 , A C → = 4 ; − 1 ⇒ ( A B ) ⃗ . ( A C ) ⃗ = 3 . 4 + 12 . ( - 1 ) = 0 ⇒ ∆ A B C vuông tại A. Trực tâm của tam giác là đỉnh A. Chọn B
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 12 2022
\(\left\{{}\begin{matrix}\overrightarrow{BA}=\left(3;-1\right)\\\overrightarrow{BC}=\left(-4;-2\right)\end{matrix}\right.\)
\(\Rightarrow cos\widehat{ABC}=cos\left(\overrightarrow{BA};\overrightarrow{BC}\right)=\dfrac{3.\left(-4\right)+1.2}{\sqrt{3^2+1^2}.\sqrt{\left(-4\right)^2+\left(-2\right)^2}}=-\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{ABC}=135^0\)
CM
26 tháng 10 2019
Chọn A.
Gọi AH là đường cao của tam giác ABC ⇒ AH ⊥ BC.
B(4;5), C(-3;2)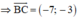 
Phương trình đường cao AH đi qua A(2;-1) nhận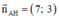 
là VTPT là:
7.(x - 2) + 3.(y + 1) = 0 ⇔ 7x - 14 + 3y + 3 = 0 ⇔ 7x + 3y - 11 = 0
Vậy phương trình đường cao AH là 7x + 3y - 11 = 0.
CM
23 tháng 6 2017
Ta có B A → = 3 ; − 1 và B C → = − 4 ; − 2 . Suy ra:
cos B A → , B C → = B A → . B C → B A → . B C → = 3. − 4 + − 1 . − 2 9 + 1 . 16 + 4 = − 2 2 ⇒ B ^ = B A → , B C → = 135 O .
Chọn D.
Lời giải:
Vì $G$ là trọng tâm $ABC$ nên:
$x_G=\frac{x_A+x_B+x_C}{3}=0$
$y_G=\frac{y_A+y_B+y_C}{3}=\frac{2}{3}$
ĐT cần tìm song song với trục tung nên nhận vecto pháp tuyến $(1,0)$
Do đó PTĐT cần tìm có dạng $1(x-0)+0(y-\frac{2}{3})=0$ hay $x=0$ hay chính là trục tung (??)