Cho hình vẽ bên :
Hãy c/m a // b bằng nhiều cách? Hãy tính số đo của các góc còn lại có trong hình?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A 1 ^ và A 2 ^ là hai góc kề bù nên A 1 ^ + A 2 ^ = 180 °
⇒ A 2 ^ = 180 ° − A 1 ^ = 180 ° − 50 ° = 130 ° B 3 ^ = B 1 ^ = A 3 ^ = A 1 ^ = 50 ° B 4 ^ = B 2 ^ = A 4 ^ = A 2 ^ = 130 ° .

Tính được M 2 ^ = M 4 ^ = N 2 ^ = N 4 ^ = 120 ° M 1 ^ = M 3 ^ = N 3 ^ = N 1 ^ = 60 °
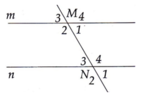

Tính được M 2 ^ = M 4 ^ = N 2 ^ = N 4 ^ = 120 ° M 1 ^ = M 3 ^ = N 3 ^ = N 1 ^ = 60 °

Tương tự 5. Tính được A 3 ^ = A 1 ^ = B 3 ^ = B 1 ^ = 60 ° A 2 ^ = A 4 ^ = B 2 ^ = B 4 ^ = 120 °

Tính được A 3 ^ = A 1 ^ = B 3 ^ = B 1 ^ = 60 ° A 2 ^ = A 4 ^ = B 2 ^ = B 4 ^ = 120 °

a) Số đo \(\widehat{xAy}\) là: 90o vì có kí hiệu vuông góc.
b) Số đo \(\widehat{x'Ay}\):
Vì \(\widehat{x'Ay}\) và \(\widehat{xAy}\) là hai góc kề bù nên
nên \(\widehat{x'Ax}\) = \(\widehat{x'Ay}\) + \(\widehat{xAy}\)
180o = \(\widehat{x'Ay}\) + 90o
\(\widehat{x'Ay}\) = 180o - 90o
\(\widehat{x'Ay}\) = 90o
c) Số đo \(\widehat{x'Ay'}\):
Vì \(\widehat{xAy}\) và \(\widehat{x'Ay'}\) là hai góc đối đỉnh
nên: \(\widehat{x'Ay'}\) = \(\widehat{xAy}\) = 90o
d) Số đo \(\widehat{xAy'}\):
Vì \(\widehat{xAy'}\) và \(\widehat{x'Ay}\) là hai góc đối đỉnh
nên \(\widehat{xAy'}\) = \(\widehat{x'Ay}\) = 90o

Câu 10:
góc A=180-130=50 độ
góc B=(180+50)/2=230/2=115 độ
góc C=180-115=65 độ
Cách 1: Xét góc A2+B1=135o+45o=180o
mà A2 và B1 là 2 góc trong cùng phía của 2 đường thẳng a và b
suy ra a//b
Cách 2: góc B4=180o-45o=135o(t/c góc kề bù)
ta có: A1 và B4 là hai góc so le trong
mà A1=B4 suy ra a//b
+) Do \(\widehat{A_1}\) và \(\widehat{A_2}\) là 2 góc kề bù
\(\Rightarrow\widehat{A_1}+\widehat{A_2}=180^o\)
hay \(\widehat{A_1}+135^o=180^o\)
\(\Rightarrow\widehat{A_1}=45^o\)
+) Do \(\widehat{B_1}\) và \(\widehat{B_2}\) là 2 góc kề bù
\(\Rightarrow\widehat{B_1}+\widehat{B_2}=180^o\)
Hay \(45^o+\widehat{B_2}=180^o\)
\(\Rightarrow\widehat{B_2}=135^o\)
Cách 1: Do \(\widehat{A_1}=\widehat{B_1}\left(=45^o\right)\)
Mà \(\widehat{A_1}\) và \(\widehat{B_1}\) là 2 góc so le trong nên a //b ( Dấu hiệu nhận biết )
Cách 2: Do \(\widehat{A_2}\)=\(\widehat{B_2}\left(=135^o\right)\)
Mà \(\widehat{A_2}\) và \(\widehat{B_2}\) là 2 góc đồng vị nên a // b ( Dấu hiệu nhận biết )
Cách 3 : Do \(\widehat{A_2}+\widehat{B_1}=135^o+45^o=180^o\)
Mà \(\widehat{A_2}\) và \(\widehat{B_1}\) là 2 góc trong cùng phía nên a // b ( Dấu hiệu nhận biết )
+) Do a // b ( cmt )
Mà \(\widehat{B_1}\) và \(\widehat{A_3}\) là 2 góc đồng vị nên \(\widehat{B_1}=\widehat{A_3}\left(=45^o\right)\)(T/c của 2 đt ss)
+) Do \(\widehat{A_2}\)và \(\widehat{A_4}\) đối đỉnh
\(\Rightarrow\widehat{A}_2=\widehat{B}_4\left(=135^o\right)\)(Tính chất góc đối đỉnh)
+) Do a // b ( cmt )
Mà \(\widehat{A}_1\) và \(\widehat{B_3}\) là 2 góc đồng vị nên \(\widehat{A_1}=\widehat{B}_3\left(=45^o\right)\)(T/c của 2 đt ss)
+) Do a // b ( cmt )
Mà \(\widehat{A}_2\) và \(\widehat{B}_4\) là 2 góc so le trong nên \(\widehat{A}_2=\widehat{B}_4\left(=135^o\right)\)(T/c của 2 đt ss)
Chú thích : cmt có nghĩa là chứng minh trên
T/c của 2 đt ss có nghĩa là Tính chất của 2 đường thẳng song song