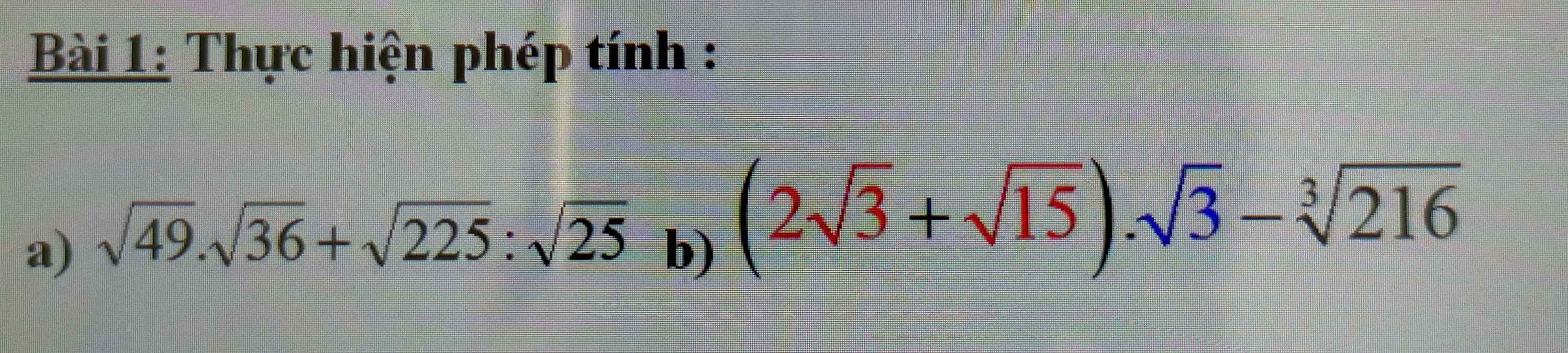giải giúp em 2 câu này với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 9 2021
\(8,=\left(2x-3\right)\left(2x+3\right)\\ 9,=\left(1-5a^2\right)\left(1+5a^2\right)\)
16 tháng 9 2021
8) \(-9+4x^2=\left(2x\right)^2-3^2=\left(2x-3\right)\left(2x+3\right)\)
9) \(1-25a^4=1-\left(5a^2\right)^2=\left(1-5a^2\right)\left(1+5a^2\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2023
10.
\(H\left(x\right)=-5x^4+10x^3-15x+1\)
\(=-5x\left(x^3-2x^2+3\right)+1\)
\(=-5x.0+1\)
\(=1\)
9.
\(P\left(x\right)-Q\left(x\right)=\left(1-a\right)x^3+x^2+x-6\)
\(P\left(x\right)-Q\left(x\right)\) là đa thức bậc 3 khi và chỉ khi \(1-a\ne0\)
\(\Rightarrow a\ne1\)
NH
1
30 tháng 4 2023
1: (x-1)^2+(y+2)^2=25
=>R=5; I(1;-2)
2: Δ'//Δ nên Δ': 3x-4y+c=0
d(I;Δ')=5
=>\(\dfrac{ \left|3\cdot1+\left(-2\right)\cdot\left(-4\right)+c\right|}{\sqrt{3^2+\left(-4\right)^2}}=5\)
=>|c+11|=25
=>c=14 hoặc c=-36
=>3x-4y+14=0 hoặc 3x-4y-36=0
3x-4y+14=0
=>VTPT là (3;-4) và (Δ') đi qua A(2;5)
=>VTCP là (4;3)
=>PTTS là x=2+4t và y=5+3t
3x-4y-36=0
=>VTPT là (3;-4) và (Δ') đi qua B(0;-9)
=>VTCP là (4;3)
PTTS là x=0+4t và y=-9+3t
NT
0
AM
10 tháng 2 2022
Ta có: \(\int\dfrac{xdx}{x^2+3}\)
Đặt \(u=x^2+3\left(u>0\right)\)
Có \(du=2xdx\)
\(\Rightarrow\int\dfrac{xdx}{x^2+3}=\)\(\int\dfrac{du}{2u}=\dfrac{1}{2}ln\left(u\right)=\dfrac{1}{2}ln\left(x^2+3\right)\)
9 tháng 3 2022
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x-2+2}{x-2}+\dfrac{1}{y+1}=3\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x-2}+\dfrac{1}{y+1}=2\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{6}{x-2}+\dfrac{3}{y+1}=6\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10}{x-2}=7\\\dfrac{2}{x-2}+\dfrac{1}{y+1}=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x-2=\dfrac{10}{7}\\\dfrac{1}{y+1}=\dfrac{3}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{24}{7}\\y=\dfrac{2}{3}\end{matrix}\right.\)
10 tháng 3 2022
Vì \(\sqrt{3\sqrt{2\sqrt{x}}}\) là số nguyên => \(3\sqrt{2\sqrt{x}}\) là số chính phương.
Mà 3 là số nguyên tố nên \(\sqrt{2\sqrt{x}}\)có dạng \(3k^2\) với k ∈ N*
\(\sqrt{2\sqrt{x}}=3k^2\Leftrightarrow2\sqrt{x}=9k^4\Leftrightarrow4x=81k^8\)\(\Leftrightarrow x=\dfrac{81}{4}k^8\)
Vì x là số có 4 chữ số => \(x\le9999\) => \(\dfrac{81}{4}k^8\le9999\Leftrightarrow k^8\le\dfrac{4444}{9}\Leftrightarrow k^8\le493\) (1)
Vì \(k\ge1\) => \(k^8\ge1\) (2)
Từ (1) và (2), ta có \(k^8\in\left\{1,256\right\}\)
-Xét \(k^8=1\Rightarrow k=1\Rightarrow x=\)\(\dfrac{81}{4}\) => Vô lí
-Xét \(k^8=256\Rightarrow k=2\Rightarrow x=5184\) t/m
Vậy x = 5184
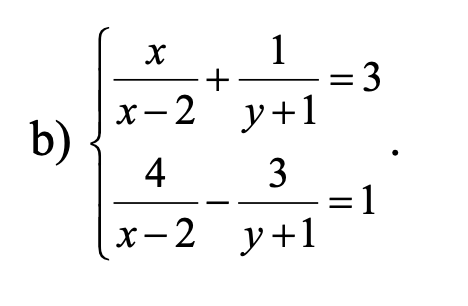
\(a,=7\cdot6+15:5=42+3=45\\ b,=6+3\sqrt{5}-6=3\sqrt{5}\)
Cảm ơn nhiều nha