Mọi người giải chi tiết giúp em với. Em cần gấp ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
18 tháng 7 2021
Gọi số sản phẩm àm 2 ng công nhân được giao là x (x∈N*, sản phẩm)
Thời gian hoàn thành công việc của người thứ nhất là: \(\dfrac{x}{40}\left(h\right)\)
Thời gian hoàn thành công việc của ngươi thứ hai là: \(\dfrac{x}{50}\left(h\right)\)
Vì ng thứ nhất hoàn thành công việc chậm hơn người thứ hai 2 giờ nên ta có PT:
\(\dfrac{x}{40}-\dfrac{x}{50}=2\)
⇔\(50x-40x=4000\)
⇔\(10x=4000\)
⇔\(x=400\)
Vậy số sản phẩm mỗi công nhân được giao là 400 (sản phẩm)
PH
1
26 tháng 11 2023
Câu 1:
\(\left\{{}\begin{matrix}y-2x< =2\\2y-x>=4\\x+y< =5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y< =2x+2\\2y>=x+4\\y< =-x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y< =2x+2\\y< =-x+5\\y>=\dfrac{1}{2}x+2\end{matrix}\right.\)
y<=2x+2
=>y-2x-2<=0
Vẽ đường thẳng y=2x+2
Khi x=0 và y=0 thì \(y-2x-2=0-0-2=-2< =0\)(đúng)
=>Miền nghiệm của BPT y<=2x+2 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y<=-x+5
=>x+y-5<=0
Khi x=0 và y=0 thì \(x+y-5=0+0-5< =0\)(đúng)
=>Miền nghiệm của BPT y<=-x+5 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y>=1/2x+2
=>\(-\dfrac{1}{2}x+y-2>=0\)
Khi x=0 và y=0 thì \(-\dfrac{1}{2}x+y-2=-\dfrac{1}{2}\cdot0+0-2=-2< 0\)
=>O(0;0) không thỏa mãn BPT \(-\dfrac{1}{2}x+y-2>=0\)
=>Miền nghiệm của BPT \(y>=\dfrac{1}{2}x+2\) là nửa mặt phẳng chứa biên nhưng không chứa điểm O(0;0)
Vẽ đồ thị:
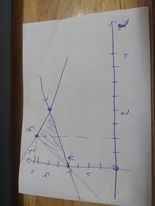
Theo hình vẽ, ta có: Miền nghiệm của hệ BPT sẽ là ΔABC, với A(0;2); B(1;4); C(2;3)
Khi x=0 và y=2 thì F=2-0=2
Khi x=1 và y=4 thì F=4-1=3
Khi x=2 và y=3 thì F=3-2=1
=>Chọn A
NM
0
20 tháng 6 2019
Ta có : \(94-42\sqrt{5}=45-2.7.3\sqrt{5}+49=\left(3\sqrt{5}\right)^2-2.7.3\sqrt{5}+7^2=\left(7-3\sqrt{5}\right)^2\)
\(94+42\sqrt{5}=\left(7+3\sqrt{5}\right)^2\)
\(\Rightarrow\sqrt{94-42\sqrt{5}}-\sqrt{94+42\sqrt{5}}\)
\(=\sqrt{\left(7-3\sqrt{5}\right)^2}-\sqrt{\left(7+3\sqrt{5}\right)^2}=7-3\sqrt{5}-7-3\sqrt{5}=-6\sqrt{5}\)
17 tháng 11 2021
\(1,\Leftrightarrow x^2-8x+16-x^2+x+12=7\\ \Leftrightarrow-7x=-21\\ \Leftrightarrow x=3\\ 2,\Leftrightarrow\left(x-4\right)^2-\left(x-4\right)=0\\ \Leftrightarrow\left(x-4\right)\left(x-5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)
17 tháng 11 2021
\(1,=3ab\left(1-2a+b\right)\\ 2,=\left(x-y\right)\left(x+y\right)-7\left(x+y\right)=\left(x+y\right)\left(x-y-7\right)\\ 3,=\left(a-5\right)\left(5a-2\right)\\ 4,=5x\left(x-3\right)-\left(x-3\right)\left(x+3\right)=\left(x-3\right)\left(4x-3\right)\\ 5,=9a^2-\left(b-2\right)^2=\left(3a-b+2\right)\left(3a+b-2\right)\\ 6,=2x^2-4x+3x-6=\left(x-2\right)\left(2x+3\right)\\ 7,=3x^2\left(2x-5\right)\\ 8,=\left(3x-5\right)\left(3x+5\right)\\ 9,=4x^2\left(x-y\right)-x\left(x-y\right)=x\left(4x-1\right)\left(x-y\right)\)
5 tháng 12 2021
\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{24\cdot12}{24+12}=8\Omega\)
\(I=\dfrac{U}{R}=\dfrac{12}{8}=1,5A\)
\(P=\dfrac{U^2}{R}=\dfrac{12^2}{8}=18W\)
\(Q_{tỏa1}=A_1=U_1\cdot I_1\cdot t=12\cdot\dfrac{12}{24}\cdot1\cdot3600=21600J\)
\(Q_{tỏa2}=A_2=U_2\cdot I_2\cdot t=12\cdot\dfrac{12}{12}\cdot1\cdot3600=43200J\)
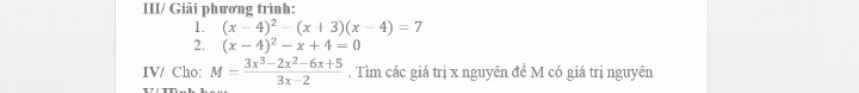
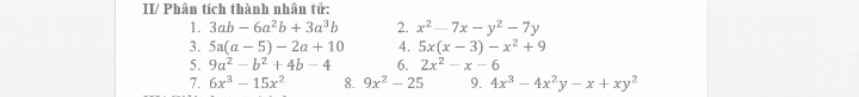
\(B=-x^2+2x-4\)
\(=-\left(x^2-2x+4\right)\)
\(=-\left(x-1\right)^2-3\le-3\forall x\)
Dấu '=' xảy ra khi x=-3