Một hộp giấy có dạng hình trụ đựng 5 quả bóng tennis, chiều cao đúng bằng 5 quả bóng tennis đặt khít vào nhau, 2 mặt đáy là hai hình tròn có kích thước đúng bằng kích thước đường tròn lớn của mỗi quả bóng. Biết mỗi quả bóng có đường kính là 6, 4cm . Tính diện tích phần giấy làm nhãn hiệu bao quanh thân hộp (diện tích xung quanh hộp).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng BĐT sau:\(2\left(a^2+b^2\right)\ge\left(a+b\right)^2\) ( dùng BĐT Bunhiacopski mà chứng minh :D )
Ta có:\(\frac{a+b}{a^2+b^2}=\frac{41}{9}\Rightarrow\frac{a^2+b^2}{a+b}=\frac{41}{9}\)
\(\Rightarrow\frac{82}{9}=\frac{2\left(a^2+b^2\right)}{a+b}\ge\frac{\left(a+b\right)^2}{a+b}=a+b\)
\(\Rightarrow a+b\le9\)
Mặt khác:\(41\left(a+b\right)=9\left(a^2+b^2\right);\left(41;9\right)=1\Rightarrow a+b⋮9\Rightarrow a+b=9\)
\(\Rightarrow a^2+b^2=41\)
Ta có hệ:\(\hept{\begin{cases}a+b=9\\a^2+b^2=41\end{cases}}\) giải cái hệ này là ra a,b nha < 3

Đường kính quả bóng tennis là
2R = 25 5 = 5.
Diện tích quả bóng:
S = 4 π . R 2 = 4 π . 5 2 2 = 25 π c m 2
Đáp án B

Chọn A
Khi đó bán kính đáy của chiếc hộp hình trụ cũng là R.
Tổng diện tích ba quả bóng bàn là:
![]()
Diện tích xung quanh của hình trụ:


Đáp án là A.
Giả sử bán kính của quả bóng bàn là r
Tổng diện tích của ba quả bóng bàn là:
S 1 = 3.4 π r 2 = 12 π r 2
Diện tích xung quanh của hình trụ là:
S 2 = 2 π r h = 2 π r .6 r = 12 π r 2
Do đó ta có S 1 S 2 = 12 π r 2 12 π r 2 = 1 .

Đáp án A
* Hướng dẫn giải: Đơn giản ta có được
S 1 = 3 ( 4 πr 2 ) = 12 πr 2 , S 2 = 12 πr 2
⇒ S 1 S 2 = 1
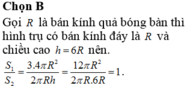



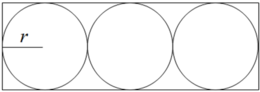

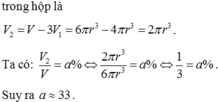
- Khoảng cách giữa 2 đáy trụ là : \(5.6,4=32\left(cm\right)\)
- Bán kính hình trụ đó là : \(6,4:2=3,2\left(cm\right)\)
-> \(S_{xungquanh}=2\pi.r.h=2\pi.32.3,2=\frac{1024\pi}{5}\left(cm^2\right)\)