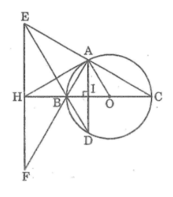
Cho tam giác ABC nội tiếp trong đường tròn ( O ) . AD là tia phân giác của góc A ( D thuộc BC) . Gọi E là giao điểm của AD với đường tròn ( O)
a) Tiếp truyến của đường tròn tại A cắt BC ở I . Chứng minh rằng tam giác IAD là tam giác cân
b) Kẻ đường kính EOF . Gọi M là giao điểm của FA với BC . Chứng minh rằng M đối xứng với D qua I


a) Có : \(\widehat{IAB}+\widehat{BAD}=\widehat{IAD}\)
mà \(\widehat{IAB}=\widehat{DAC}\) ( hệ quả của góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung ) ; \(\widehat{BAD}=\widehat{DAC}\)
=> \(\widehat{IAD}=\widehat{DAC}+\widehat{ACD}\)
Mặt khác : \(\widehat{ADI}=\widehat{DAC}+\widehat{ACD}\) ( tính chất góc ngoài )
=> \(\widehat{IAD}=\widehat{IDA}\Rightarrow\Delta IAD\) cân tại I => IA = ID
b) Có \(\widehat{EAF}\) là góc nội tiếp chắn nửa đường tròn
=> \(\widehat{EFA}=90^o\Rightarrow\widehat{MAD}=90^o\)
Có: \(\widehat{AMD}+\widehat{ADM}=\widehat{MAI}+\widehat{IAD}=90^o\)
mà \(\widehat{IAD}=\widehat{IDA}\)
=> \(\widehat{IMA}=\widehat{IAM}\Rightarrow\Delta AIM\) cân tại I
=> MI = AI mà IA = ID
=> MI = ID
hay M đối xứng với D qua I