Gọi S là tập hợp các giá trị nguyên m nằm trong khoảng (-2019; 2019) để bất phương trình \(\left|4x-2m-\frac{1}{2}\right|>-x^2+2x+\frac{1}{2}-m\) đúng với mọi số thực x. Tìm số các phần tử tập hợp S.
Mọi người giúp mình với vì ngày mai mình cần nộp để lấy điểm ạ. Cảm ơn sự giúp đỡ của mọi người rất nhiều ạ!



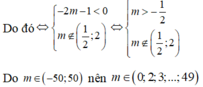





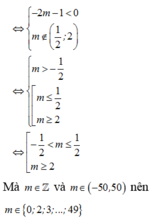

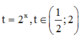
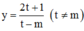

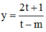

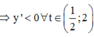 và
và 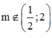
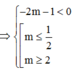
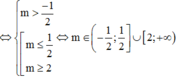
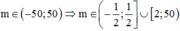


ĐK: \(-x^2+2x+\frac{1}{2}-m\ge0\)
\(pt\Leftrightarrow\left[{}\begin{matrix}4x-2m-\frac{1}{2}>-x^2+2x+\frac{1}{2}-m\\4x-2m-\frac{1}{2}< x^2-2x-\frac{1}{2}+m\end{matrix}\right.\)
Xét từng bpt một nhé:
\(x^2+2x-1-m>0\) (1)
Để (1) đúng với mọi x thì \(\Delta< 0\Leftrightarrow1+1+m< 0\Leftrightarrow m< -2\)
\(x^2-6x+3m>0\) (2)
Để (2) đúng với mọi x thì \(\Delta< 0\Leftrightarrow9-3m< 0\Leftrightarrow m>3\)
\(\Rightarrow\left[{}\begin{matrix}m>3\\m< -2\end{matrix}\right.\)
\(\Rightarrow S=\left(-2019;-2\right)\cup\left(3;2019\right)\)
Tự đếm xem có bao nhiêu phần tử nha cậu :))