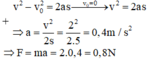Xe hơi có khối lượng 1,5Tấn chuyển động nhanh dần đều trên mặt đường nằm ngang từ trạng thái đứng yên. Sau 5 giây chuyển động xe đạt tốc độ 36km/h.
a. Tính gia tốc của xe.
b. Tính hợp lực tác dụng vào xe.
c. Tính lực kéo của động cơ. Cho biết lực cản không đổi và bằng 200N.
d. Tính vận tốc của xe sau 10 giây chuyển động.