một cầu trượt có đường lên AB dài 4,5m độ cao AH 3,6m độ dài BC là 7,5m CD là 2m tính độ dài đường trượt ACD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 7 2018
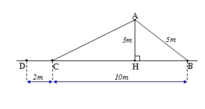
+ ΔAHB vuông tại H
Theo định lí Py–ta- go ta có
HB2 = AB2 – AH2 = 52 – 32 =25 - 9 =16
Suy ra HB = 4 (cm)
Suy ra HC = BC – HB = 10 - 4 = 6(cm)
+ ΔAHC vuông tại H
Theo định lí Py-ta-go ta có
AC2 = AH2 + HC2 = 32 + 62 = 9 + 36 = 45.
Suy ra AC = √45 ≈ 6,7(m)
Độ dài đường trượt ACD bằng: 6,7 + 2= 8,7 (m)
Và hai lần đường lên BA bằng 5.2 =10 (m)
Đo độ dài đường trượt ACD chưa bằng hai lần đườg lên BA
Vậy bạn Mai nói sai, bạn Vân nói đúng.
DN
20 tháng 4 2017
Xét tam giác vuông AHB (^AHB = 90°) ta có:
AB2 = AH2 + HB2 (vì bình phương cạnh huyền bằng tổng bình phương 2 cạnh góc vuông).
hay 52 = 32 + HB2
=> HB2 = 52 - 32 = 25 - 9 = 16.
HB = \(\sqrt{16}\) = 4.
Vậy HB = 4m.
Độ dài cạnh CH là:
CH = BC - HB
hay CH = 10 - 4 = 6 (m)
Vậy cạnh CH = 6m.
Xét tam giác vuông AHC (^AHC = 90°) ta có:
AC2 = AH2 + CH2
hay AC2 = 32 + 62 = 9 + 36 = 45.
AC = \(\sqrt{45}\approx7.\)
Vậy AC \(\approx7m\).
Độ dài ACD là:
ACD = AC + CD
hay ACD = 7 + 2 = 9 (m).
Vậy ACD = 9m.
2 lần BA là:
5.2 = 10 (m)
Vậy 2 lần BA = 10m.
Mà ACD < BA (9 < 10) nên đường trượt ACD ko gấp hơn hai lần đường lên BA.
Vậy bạn Mai nói sai, bạn Vân nói đúng.
14 tháng 8 2023
1: Chiều cao của cột đèn là:
7,5*tan42\(\simeq6,75\left(m\right)\)
CM
26 tháng 5 2018
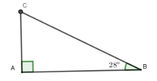
Ta có độ dài của mặt cầu trượt là AB, AC = 2,1m và A B C ^ = 28 0
Xét tam giác ACB vuông tại A có:
BC = AB : sin B = 2,1 : sin 28 0 ≈ 4,47m
Vậy độ dài của mặt cầu trượt là 4,47m
Đáp án cần chọn là: D
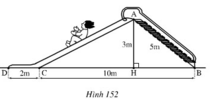
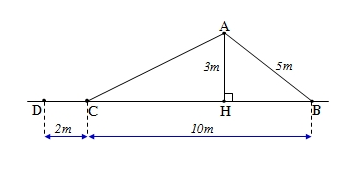
+ Xét \(\Delta ABH\) vuông tại \(H\left(gt\right)\) có:
\(AB^2=AH^2+BH^2\) (định lí Py - ta - go).
=> \(\left(4,5\right)^2=\left(3,6\right)^2+BH^2\)
=> \(BH^2=\left(4,5\right)^2-\left(3,6\right)^2\)
=> \(BH^2=20,25-12,96\)
=> \(BH^2=7,29\)
=> \(BH=2,7\left(m\right)\) (vì \(BH>0\)).
+ Ta có: \(BH+CH=BC.\)
=> \(2,7+CH=7,5\)
=> \(CH=7,5-2,7\)
=> \(CH=4,8\left(m\right).\)
+ Xét \(\Delta ACH\) vuông tại \(H\left(gt\right)\) có:
\(AC^2=AH^2+CH^2\) (định lí Py - ta - go).
=> \(AC^2=\left(3,6\right)^2+\left(4,8\right)^2\)
=> \(AC^2=12,96+23,04\)
=> \(AC^2=36\)
=> \(AC=6\left(m\right)\) (vì \(AC>0\)).
Độ dài đường trượt \(ACD\) là:
\(AC+CD=6+2=8\left(m\right).\)
Vậy độ dài đường trượt \(ACD\) là: \(8\left(m\right).\)
Chúc bạn học tốt!