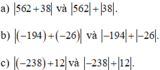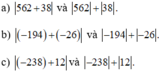Nêu nhận xét về cách tính giá trị tuyệt đối của 1 số
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 5 2021
Cách tính : a thuộc z thì giá trị tuyệt đối của a thuộc z = a ( đối với dạng phép tính thì chia ra làm 2 TH )
Nhận xét: Giá trị tuyệt đối (tiếng Anh: Absolute value) - còn thường được gọi là mô-đun (modulus) của một số thực x được viết là |x|, là giá trị của nó nhưng bỏ dấu. Như vậy |x| = -x nếu x là số âm (-x là số dương), và |x| = x nếu x là số dương, và |0| =0. Giá trị tuyệt đối của một số có thể hiểu là khoảng cách của số đó đến số 0.
Trong toán học, việc sử dụng giá trị tuyệt đối có trong hàng loạt hàm toán học, và còn được mở rộng cho các số phức, véctơ, trường,... liên hệ mật thiết với khái niệm giá trị.
Đồ thị của một hàm số có các biến số nằm trong dấu "giá trị tuyệt đối" thì luôn luôn nằm phía trên của trục hoành.
YA
2
28 tháng 5 2021
Giá trị tuyệt đối của 1 số nguyên: A ko thể là một số nguyên âm vì |A| luôn ko âm. Giá trị tuyệt đối của một số nguyên A có thể là số 0 nếu A=0
31 tháng 5 2021
Giá trị tuyệt đối của 1 số nguyên: A ko thể là một số nguyên âm vì |A| luôn ko âm. Giá trị tuyệt đối của một số nguyên A có thể là số 0 nếu A=0
CM
27 tháng 8 2017
d) Giá trị tuyệt đối của một tổng hai số nguyên luôn nhỏ hơn hoặc bằng tổng hai giá trị tuyệt đối của chúng
CM
2 tháng 12 2019
d) Giá trị tuyệt đối của một tổng hai số nguyên luôn nhỏ hơn hoặc bằng tổng hai giá trị tuyệt đối của chúng.
14 tháng 9 2018
1) Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức , ta phải đổi dấu số hạng đó
Với mọi \(x,y,z\in Q:x+y=z\Rightarrow x=z-y\)
2) Với \(x=\frac{a}{b},y=\frac{c}{d}\) Ta có : \(x.y=\frac{a}{b}.\frac{c}{d}=\frac{a.c}{b.d}\)
3) Với mọi \(x\in Q\) ta luôn có : \(\left|x\right|\ge0,\left|x\right|=\left|-x\right|\) và \(\left|x\right|\ge x\)
PT
1
CM
10 tháng 3 2018
Giá trị tuyệt đối của tích hai số nguyên khác dấu là một số nguyên dương
- Dấu của tích hai số nguyên khác dấu là dấu âm " – "
DR
0
18 tháng 1 2018
(-5) . 3 = -15
2.(-6) = -12
Nhận xét:
Dấu của tích hai số nguyên khác dấu luôn là dấu âm
Giá trị tuyệt đối của số âm hay số dương đều có kết quả là số dương