Cho tam giác ABC cân tại A.Kẻ AH vuông góc BC tại H .Trên tia đối của HA lấy điểm M sao cho AH=HM. a) Chứng minh tam giác ABH=tam giác MBH. b) Trên tia đối của tia CA lấy điểm N sao cho CA=CN.Chứng minh tam giác CMN cân. c) Chứng minh AM vuông góc với MN.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 12 2023
a: Xét ΔCAB và ΔCNM có
CA=CN
\(\widehat{ACB}=\widehat{NCM}\)(hai góc đối đỉnh)
CB=CM
Do đó: ΔCAB=ΔCNM
=>\(\widehat{CAB}=\widehat{CNM}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//MN
b:
Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC
Xét ΔHAC vuông tại H và ΔKNC vuông tại K có
AC=NC
\(\widehat{HCA}=\widehat{KCN}\)(hai góc đối đỉnh)
Do đó: ΔHAC=ΔKNC
=>HC=KC
mà HB=HC
nên HB=KC
Xét ΔABH vuông tại H và ΔNCK vuông tại K có
BH=CK
\(\widehat{ABH}=\widehat{NCK}\)\(\left(=\widehat{ACB}\right)\)
Do đó: ΔABH=ΔNCK
19 tháng 2 2020
Áp dụng đl Pi ta go đảo cho Tam giác ABC
=>AB2+CA2=BC2
=>152+362=392
=>1521=1521
=>Tam giác ABC vuông tại A
Áp dụng đl pi ta go cho tam giác ABH
=>AB2=AH2+BH2
=>152=92+BH2
=>BH2=225-81=144=122
=>BH=12
Vậy...
3 tháng 12 2021
1: Xét ΔHAC vuông tại H và ΔHDC vuông tại H có
CH chung
HA=HD
Do đó: ΔHAC=ΔHDC
Suy ra: CA=CD
25 tháng 12 2021
1: Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAD cân tại C
hay CA=CD
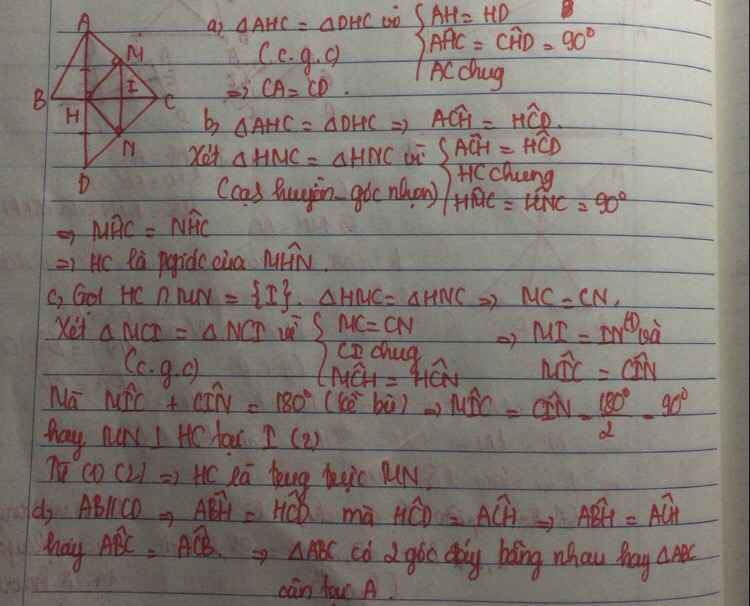
a,Ta có:
\(AH\perp BC\) nên \(\widehat{AHB}\) +90 độ.
Vì M là tia đối của HA nên \(\widehat{MHB}\)= 90 độ.
Xét \(\Delta ABH\) và \(\Delta MBH\)có
AH = MH (gt)
\(\widehat{AHB}\) = \(\widehat{MHB}\) (= 90 độ )
BH : cạnh chung
\(\Rightarrow\Delta ABH=\Delta MBH\)( c.g.c )
b,Xét \(\Delta AHCv\text{à}\Delta MHC\)Ta có:
AH = HM (gt)
\(\widehat{AHC}\)= \(\widehat{MHC}\)(= 90 độ)
HC : cạnh chung
\(\Rightarrow\Delta AHC=\Delta MHC\)( c.g.c)
\(\Rightarrow\)AC=CM ( t/ứ)
Mà AC = CN (gt) và CM = AC (cmt)
nên CM = CN
\(\Rightarrow\Delta CMN\)cân