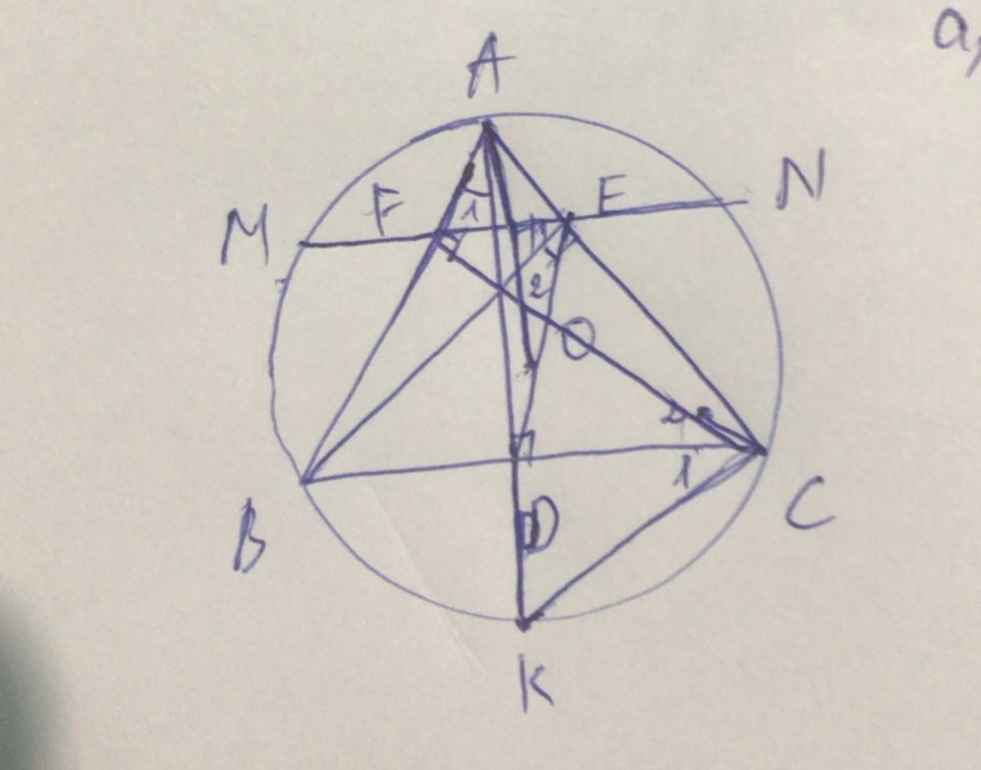
Cho tam giác đều ABC nội tiếp đường tron (O).Các đường thẳng BO và CO lần lượt cắt (O) tại E và F
1, Chứng minh AF//BE
2, Gọi M là 1 điểm trên đoạn AE (M khác A,E) đường thẳng FM cắt BE kéo dài tại N, OM cắt AN tại G. Chứng minh
a,AF2=AM.ON
b, Tứ giác AGEO nội tiếp





1. Do ΔABC đều, BE và CF là tia phân giác của góc B, góc C nên ∠B1 = ∠B2 = ∠C1 = ∠C2 ⇒ AE = AF = BF = CE
∠FAB = ∠B1 => AF//BE
2. (1,0 điểm)
Tương tự câu 1) ta có AE//CF nên tứ giác AEOF là hình bình hành mà →AE = AF => →AE = AF nên tứ giác AEOF là hình thoi.
DOFN và DAFM có ∠FAE = ∠FOE (2 góc đối của hình thoi)
∠AFM = ∠FNO (2 góc so le trong)
=> ΔAFM đồng dạng với ΔONF (g-g)
⇒ AF/ON = AM/OF ⇔ AF.OF = AM.ON
mà AF = OF nên AF² = AM.ON
3. (1,0 điểm)
Có ∠AFC = ∠ABC = 600 và AEOF là hình thoi => ΔAFO và ΔAEO là các tam giác đều => AF=DF=AO
=> AO² = AM.MO
⇔ AM/AO = AO/ON và có ∠OAM = ∠AOE = 600 => ΔAOM và ΔONA đồng dạng.
=> ∠AOM = ∠ONA
Có 60º = ∠AOE = ∠AOM + ∠GOE = ∠ANO + GAE
=> ∠GAE = ∠GOE
mà hai góc cùng nhìn GE nên tứ giác AGEO nội tiếp