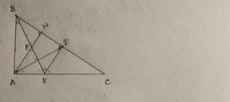
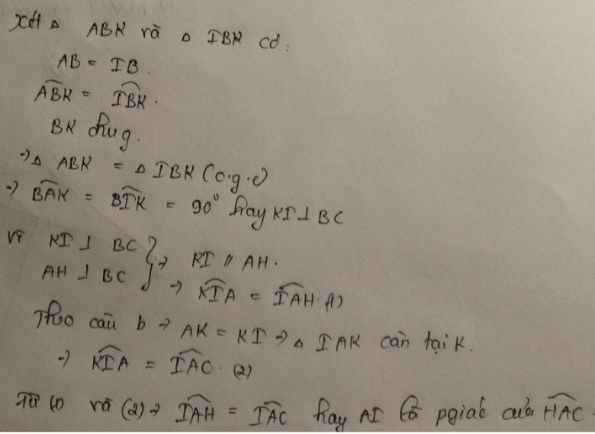cho tam giác ABC vuông tại A,lấy điểm K thuộc cạnh AC,kẻ KH vuông góc với bc tại h.cm cos C=AH/BK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 8 2021
bn tham khảo tại đây;
https://olm.vn/hoi-dap/detail/256733768368.html
DT
9 tháng 3 2022
Có gì khong hiểu hỏi lại cj nhé:
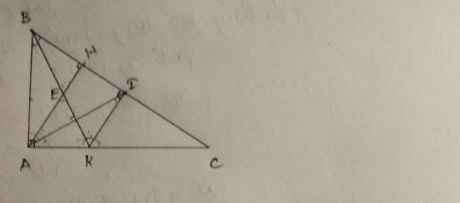
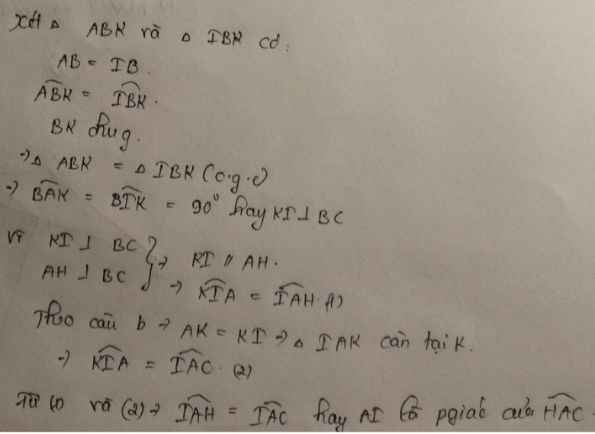
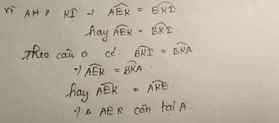
a, b ,c lần lượt từ trên xuống.
21 tháng 6 2023
a: Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AH=AK
AD chung
=>ΔAHD=ΔAKD
b: AK=AH
DH=DK
=>AD là trung trực của HK
5 tháng 5 2021
b) Ta có: KI\(\perp\)BC(gt)
AH\(\perp\)BC(gt)
Do đó: KI//AH(Định lí 1 từ vuông góc tới song song)
Suy ra: \(\widehat{HAI}=\widehat{KIA}\)(hai góc so le trong)(1)
Ta có: ΔABK=ΔIBK(cmt)
nên KA=KI(hai cạnh tương ứng)
Xét ΔKAI có KA=KI(cmt)
nên ΔKAI cân tại K(Định nghĩa tam giác cân)
Suy ra: \(\widehat{KAI}=\widehat{KIA}\)(hai góc ở đáy)(2)
Từ (1) và (2) suy ra \(\widehat{HAI}=\widehat{KAI}\)
\(\Leftrightarrow\widehat{HAI}=\widehat{CAI}\)
Suy ra: AI là tia phân giác của \(\widehat{HAC}\)(Đpcm)
5 tháng 5 2021
a) Xét ΔABK vuông tại A và ΔIBK vuông tại I có
BK chung
\(\widehat{ABK}=\widehat{IBK}\)(BK là tia phân giác của \(\widehat{ABI}\))
Do đó: ΔABK=ΔIBK(Cạnh huyền-góc nhọn)
8 tháng 1 2024
Xét ΔBAK vuông tại A và ΔBHK vuông tại H có
BK chung
KA=KH
Do đó: ΔBAK=ΔBHK
=>BA=BH
=>B nằm trên đường trung trực của AH(1)
Ta có: KA=KH
=>K nằm trên đường trung trực của AH(2)
Từ (1) và (2) suy ra BK là đường trung trực của AH
=>BK\(\perp\)AH