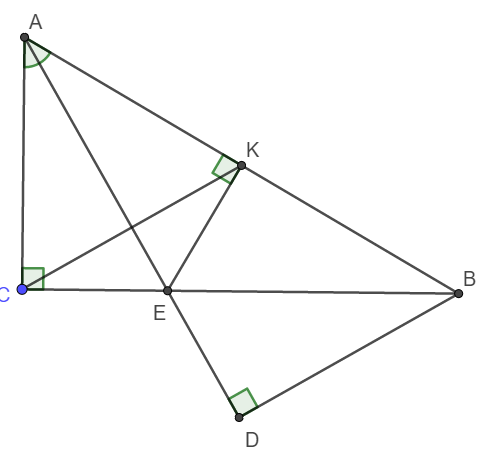
Cho tam giác ABC vuông tại C có A= 60 độ và đường phân giác của BAC cắt BC tại E. Kẻ EK vuông góc AB tại K ( K € AB ). Kẻ BD vuông góc AE tai D ( D € AE ). Chứng minh
a) Tam giác ACE = Tam giác AKE
b) AE là đường trung trực của đoạn thẳng CK
c) KA = KB
d) EB > EC

a) Xét t/g vuông ACE và t/g vuông AKE ta có:
gECA=gEKA=90o
=>EA là cạnh huyền chung
Mà gCAE=gKAE( vì AE là tia p/g của góc A)
Nên t/gACE=t/gAKE(GH-GN)
=>AC=AK (2 cạnh tương ứng)
b)Lại có AC=AK (cmt)
=>A nằm trên đường trung trực của KC(1)
=>t/gAK=t/AE
=>E nằm trên đường trung trực của KC (2)
Từ (1)và (2) => AE là đường trung trực của KC
c)Ta có trong t/g vuông BCA thì
gB+gA=90o
=>gB-gA(90o)-60o=30o
=>EAB=90o
=>Ek vuông vs BA
Mà cũng là đường trung trực của AEB
Nên KA=KB.
d) Thấy trong t/g vuông BEK : EB>EK
Mà KA=KB
KA=KC
=>BK=AC hay EB=AC
=>EB>EC
=>đpcm.
Hình sai sai