Tìm m để bất phương trình m(2x-1) ≥ 2x+1 có tập nghiệm \([1;+\infty)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 2 2021
1.
\(\Leftrightarrow\left(m^2+4\right)x\ge2-m\)
Do \(m^2+4>0\) ; \(\forall m\)
\(\Rightarrow x\ge\dfrac{2-m}{m^2+4}\)
2.
\(\Leftrightarrow2mx-2x\ge m-1\Leftrightarrow2\left(m-1\right)x\ge m-1\)
- Với \(m>1\Rightarrow m-1>0\)
\(\Rightarrow x\ge\dfrac{m-1}{2\left(m-1\right)}\Leftrightarrow x\ge\dfrac{1}{2}\) \(\Rightarrow D=[\dfrac{1}{2};+\infty)\)
- Với \(m< 1\Rightarrow m-1< 0\Rightarrow x\le\dfrac{m-1}{2\left(m-1\right)}\Leftrightarrow x\le\dfrac{1}{2}\) \(\Rightarrow D=(-\infty;\dfrac{1}{2}]\)
- Với \(m=1\Leftrightarrow0\ge0\Rightarrow D=R\)
Quan sát 3 TH ta thấy không tồn tại m để tập nghiệm của BPT là \([1;+\infty)\)
24 tháng 2 2022
2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)
28 tháng 7 2023
3:
x^2-2x+1-m^2<=0
=>(x-1)^2-m^2<=0
=>(x-1)^2<=m^2
=>-m<=x-1<=m
=>-m+1<=x<=m+1
mà x thuộc [-1;2]
nên -m+1>=-1 và m+1<=2
=>-m>=-2 và m<=1
=>m<=2 và m<=1
=>m<=1
12 tháng 5 2017
bpt (1) : x> \(\frac{2m}{3m-1}\); bpt (2) : x > \(\frac{m}{2}\)
de 2 bpt co cung tap nghiem thi \(\frac{2m}{3m-1}\)= \(\frac{m}{2}\)(3) voi dk m # \(\frac{1}{3}\)
giai pt (3) tim duoc m= 0 , m = \(\frac{5}{3}\)thoa dieu kien m # \(\frac{1}{3}\)
AM
25 tháng 1 2022
\(\left\{{}\begin{matrix}2x-1>x+1\\2x-1>m\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x>2\\2x-1>m\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2x>4\\2x-1>m\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2x-1>3\\2x-1>m\end{matrix}\right.\)
\(\Rightarrow m\le3\)
25 tháng 1 2022
Mình nghĩ chắc là chưa đúng đâu vì với m = 15 thì ta đc :
\(\left\{{}\begin{matrix}2x-1>x+1\\2x-1>15\end{matrix}\right.\) \(\Leftrightarrow\)\(\left\{{}\begin{matrix}x>2\\x>8\end{matrix}\right.\)\(\Leftrightarrow\)x > 8
TN: S =\((\) 8;\(+\infty\)\()\)
Như vậy với m = 15 thì bất phương trình đã cho có nghiệm trong khi bạn giải với m \(\le\) 3 thì bất phương trình đã cho mới có nghiệm
HT
0
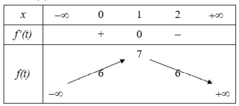
Với \(x\ge1\Rightarrow2x-1>0\)
BPT tương đương: \(m\ge\frac{2x+1}{2x-1}=1+\frac{2}{2x-1}\)
Để BPT có tập nghiệm \(x\ge1\Rightarrow m=\max\limits_{x\ge1}\left(1+\frac{2}{2x-1}\right)=3\)
Vậy \(m=3\)