Cho tam giác ABC vuông tại A. Một đường thẳng cắt hai cạnh AB, AC ở D và E. Chứng minh CD2 - CB2 = ED2 - EB2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 2 2022
Áp dụng định lý Pitago cho tam giác vuông ACD:
\(CD^2=AD^2+AC^2\)
Áp dụng định lý Pitago cho tam giác vuông ABC:
\(CB^2=AB^2+AC^2\)
\(\Rightarrow CD^2-CB^2=AD^2+AC^2-AB^2-AC^2=AD^2-AB^2\) (1)
Áp dụng định lý Pitago cho tam giác vuông ADE:
\(ED^2=AD^2+AE^2\)
Áp dụng định lý Pitago cho tam giác vuông ABE:
\(EB^2=AB^2+AE^2\)
\(\Rightarrow ED^2-EB^2=AD^2+AE^2-AB^2-AE^2=AD^2-AB^2\) (2)
(1);(2) \(\Rightarrow CD^2-CB^2=ED^2-EB^2\)
15 tháng 2 2022
Ta cần CM: \(CD^2-CB^2=ED^2-EB^2\Leftrightarrow CD^2-AB^2-AC^2=ED^2-EB^2\Leftrightarrow EB^2-AB^2=ED^2-\left(CD^2-AC^2\right)\Leftrightarrow AE^2=ED^2-AD^2\left(luônđúng\right)\) (vì các tam giác ACD, ABE,ADE đều vuông tại A) \(\Rightarrowđpcm\)
6 tháng 2 2022
a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD
nên DB=DC
b: BE⊥AC
DC⊥AC
Do đó: BE//DC
c: \(\widehat{EBC}=\widehat{DCB}\)
mà \(\widehat{DCB}=\widehat{DBC}\)
nên \(\widehat{EBC}=\widehat{DBC}\)
hay BC là tia phân giác của góc EBD
d: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
Ta có: DB=DC
nên D nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AD vuông góc BC
16 tháng 1 2021
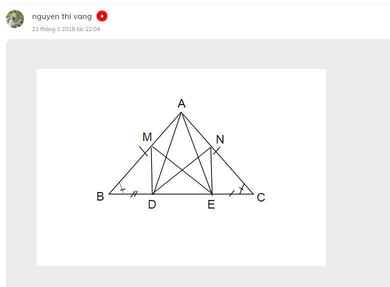
a) Xét tứ giác ADME có
ME//AD(gt)
MD//AE(gt)
Do đó: ADME là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành ADME có \(\widehat{EAD}=90^0\)(\(\widehat{BAC}=90^0,E\in AC,D\in AB\))
nên ADME là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Ta có: ADME là hình chữ nhật(cmt)
nên ED=AM(Hai đường chéo trong hình chữ nhật ADME)
mà ED=5cm(gt)
nên AM=5cm
Ta có: ΔABC vuông tại A(gt)
mà AM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(AM=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
\(\Leftrightarrow BC=2\cdot AM=2\cdot5=10\left(cm\right)\)
Xét ΔABC có AH là đường cao ứng với cạnh BC(gt)
nên \(S_{ABC}=\dfrac{AH\cdot BC}{2}=\dfrac{4.8\cdot10}{2}=24\left(cm^2\right)\)
c) Xét ΔABC có
M là trung điểm của BC(gt)
ME//AB(gt)
Do đó: E là trung điểm của AC(Định lí 1 về đường trung bình của tam giác)
Xét ΔABC có
M là trung điểm của BC(gt)
MD//AC(gt)
Do đó: D là trung điểm của AB(Định lí 1 về đường trung bình của tam giác)
Ta có: ΔAHB vuông tại H(AH⊥BC tại H)
mà HD là đường trung tuyến ứng với cạnh huyền AB(D là trung điểm của AB)
nên \(HD=\dfrac{AB}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(AD=\dfrac{AB}{2}\)(D là trung điểm của AB)
nên HD=AD
Ta có: ΔAHC vuông tại H(AH⊥BC tại H)
mà HE là đường trung tuyến ứng với cạnh huyền AC(E là trung điểm của AC)
nên \(HE=\dfrac{AC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(AE=\dfrac{AC}{2}\)(E là trung điểm của AC)
nên HE=AE
Xét ΔEAD và ΔEHD có
EA=EH(cmt)
ED chung
AD=HD(cmt)
Do đó: ΔEAD=ΔEHD(c-c-c)
⇒\(\widehat{EAD}=\widehat{EHD}\)(hai góc tương ứng)
mà \(\widehat{EAD}=90^0\)(\(\widehat{BAC}=90^0\), D∈AB, E∈AC)
nên \(\widehat{EHD}=90^0\)
hay HD⊥HE(đpcm)
HN
5 tháng 6 2017
Xét hai tam giác KAD và BAE có:
\(\widehat{KAD}=\widehat{BAE}\left(=90^o\right)\)
AD = AE (gt)
\(\widehat{D_1}=\widehat{E_1}\) (cùng phụ với góc K)
Vậy: \(\Delta KAD=\Delta BAE\left(g-c-g\right)\)
Suy ra: AK = AB (hai cạnh tương ứng)
Ta lại có AB = AC
Do đó: AK = AC.
HK
28 tháng 8 2021
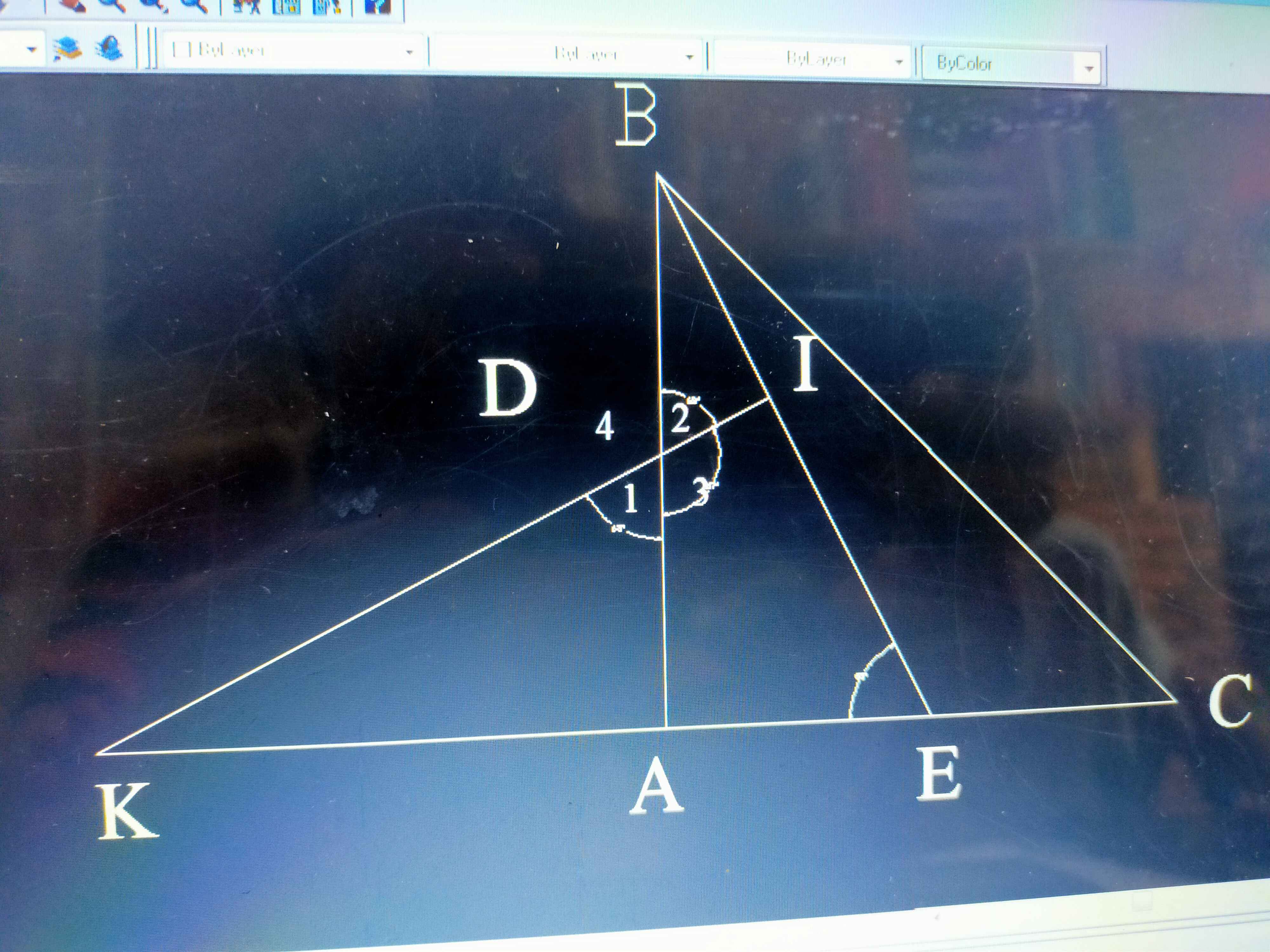Xet tứ giác ADIE ta có: góc D3+ E =180
> D3=180- E.
> D4=180-D1
[ Góc D3 =D4 (đối đỉnh)]
>> góc D1= E.
xét tam giác ABE và tam giác KAD. Có góc D1=E, cạnh AD=AE,
---> Tam giác ABE = tam giác KAD.
-->> AB =AK
> AB=AC=KA
AK=AC.
>>
16 tháng 3 2016
(mình k pk kẻ hình bn nhé)
ta có Scbe=1/2*AB*EC=1/2*ED*BC
suy ra AB.EC=BC.DE
Áp dụng định lí pytago vào ΔADE vuông tại A, ta được
\(ED^2=AE^2+AD^2\)
Áp dụng định lí pytago vào ΔABE vuông tại A, ta được
\(BE^2=AE^2+AB^2\)
Áp dụng định lí pytago vào ΔABC vuông tại A, ta được
\(BC^2=AB^2+AC^2\)
Áp dụng định lí pytago vào ΔACD vuông tại A, ta được
\(CD^2=AC^2+AD^2\)
Ta có: \(CD^2+EB^2=\left(AC^2+AD^2\right)+\left(AE^2+AB^2\right)=\left(AD^2+AE^2\right)+\left(AB^2+AC^2\right)=ED^2+CB^2\)
hay \(CD^2-CB^2=ED^2-EB^2\)(đpcm)
+ Xét \(\Delta ACD\) vuông tại \(A\left(gt\right)\) có:
\(CD^2=AC^2+AD^2\) (định lí Py - ta - go) (1).
+ Xét \(\Delta ADE\) vuông tại \(A\left(gt\right)\) có:
\(ED^2=AE^2+AD^2\) (định lí Py - ta - go) (2).
+ Xét \(\Delta ABC\) vuông tại \(A\left(gt\right)\) có:
\(CB^2=AC^2+AB^2\) (định lí Py - ta - go) (3).
+ Xét \(\Delta AEB\) vuông tại \(A\left(gt\right)\) có:
\(EB^2=AE^2+AB^2\) (định lí Py - ta - go) (4).
Trừ vế (1) với (3) và trừ vế (2) với (4) ta được:
\(\left\{{}\begin{matrix}CD^2-CB^2=AC^2-AC^2+AD^2-AB^2=AD^2-AB^2\\ED^2-EB^2=AE^2-AE^2+AD^2-AB^2=AD^2-AB^2\end{matrix}\right.\)
\(\Rightarrow CD^2-CB^2=ED^2-EB^2\left(đpcm\right).\)
Chúc bạn học tốt!