viết đa thức sau dưới dạng một phân thức đại số với tử và mẫu là đa thức có hai hạng tử
B=<x+1><x mũ 2+1><x mũ 4 +1>......<x mũ 32+1>
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
13 tháng 7
Lời giải:
$x^6-x^4+x^2-1=x^4(x^2-1)+(x^2-1)=(x^2-1)(x^4+1)$
$=\frac{(x^2-1)(x^2+1)(x^4+1)}{x^2+1}=\frac{(x^4-1)(x^4+1)}{x^2+1}=\frac{x^8-1}{x^2+1}$
CM
20 tháng 4 2019
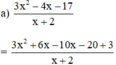
(Tách -4x = 6x – 10x để nhóm với 3x2 xuất hiện x + 2)
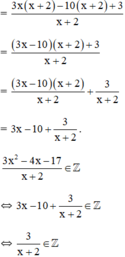
⇔ x + 2 ∈ Ư(3) = {±1; ±3}
+ x + 2 = 1 ⇔ x = -1
+ x + 2 = -1 ⇔ x = -3
+ x + 2 = 3 ⇔ x = 1
+ x + 2 = -3 ⇔ x = -5
Vậy với x = ±1 ; x = -3 hoặc x = -5 thì phân thức có giá trị nguyên.
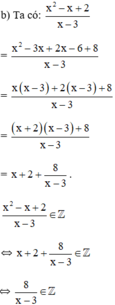
⇔ x – 3 ∈ Ư(8) = {±1; ±2; ±4; ±8}
+ x – 3 = 1 ⇔ x = 4
+ x – 3 = -1 ⇔ x = 2
+ x – 3 = 2 ⇔ x = 5
+ x – 3 = -2 ⇔ x = 1
+ x – 3 = 4 ⇔ x = 7
+ x – 3 = -4 ⇔ x = -1
+ x – 3 = 8 ⇔ x = 11
+ x – 3 = -8 ⇔ x = -5.
Vậy với x ∈ {-5; -1; 1; 2; 4; 5; 7; 11} thì giá trị phân thức là số nguyên.
28 tháng 12 2017
a, \(\frac{2x+1}{2x^2-5x-3}\)
b, \(\frac{2x+1}{2x^2-5x-3}\)
\(=\frac{2x+1}{2x^2+x-6x-3}\)
\(=\frac{2x+1}{x\left(2x+1\right)-3\left(2x+1\right)}\)
\(=\frac{2x+1}{\left(2x+1\right)\left(x-3\right)}\)
\(=\frac{1}{x-3}\)
CT
4 tháng 4 2017
Giả sử ta có : A(x) = 3x + 67 ; B(y) = y2 - 11 + 2y3
Thì : A(1) = 3.1 + 67 = 70
B(1) = 12 - 11 + 2.13 = - 8
Vậy thì tổng các hệ số của hạng tử trong đa thức chính là tổng các hạng tử của đa thức có biến là 1 .
Sau đó thì bạn thay 1 vào P(x) rồi tìm được kết quả là 1
Cái chính là hiểu bạn chất vấn đề , còn chỗ giả sử kia không phải ghi vào vở đâu nhé !
Chúc bạn học chăm !!!