Cho tam giác ABC nhọn. Gọi M là trung điểm của BC, trên tia đối của tia MA lấy điểm N sao cho MN = MA
a) Chứng minh tứ giác ABNC là hình bình hành.
b) Nếu tam giác ABC vuông cân tại A thì tứ giác ABNC là hình gì ? Vì sao ?
c) Gọi K là trung điểm của AC, H là giao điểm của BK và AM
Chứng minh: SΔHBC = \(\frac{1}{3}\)SΔABC



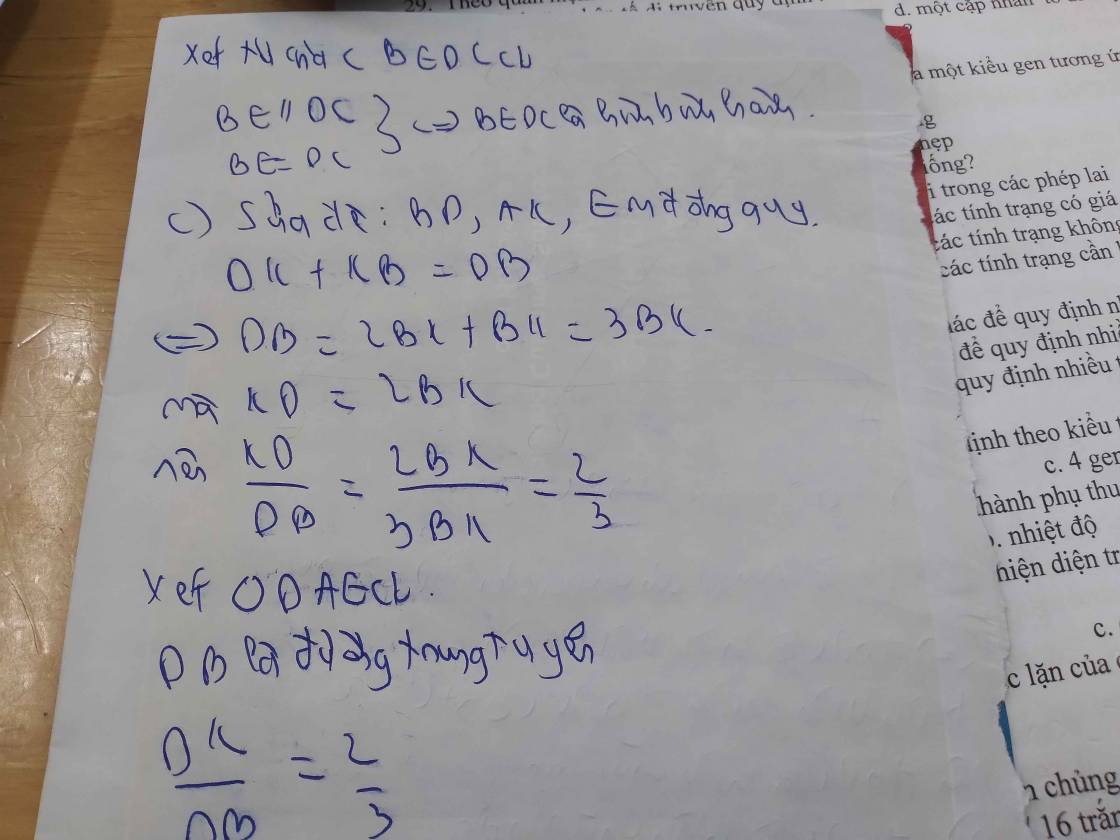

a,Vì MN=MA (gt)=> M là trung điểm của AN
xét tứ giác ABNC có; AN và BC là hai đường chéo cắt nhau tại M
M là trung điểm của BC (gt)
M là trung điểm của AN (cmt)
=> ABNC là hình bình hành
b, Vì tgABC vuông cân tại A => AB=AC;gBAC=90độ
vì ABNC là hình bình hành (cmt) có AB = AC
=> ABNC là hình thoi
xét hình thoi ABNC có gBAC = 90 độ => ABNC là hình vuông