Question

[địt mẹ mày]

Cho tam giác ABC vuông tại A. Kẻ đường phân giác BD, kẻ DE vuông góc BC

a) Chứng minh rằng: BD là trung trực của AE và AD<DC.

b) Tia BD cắt FC tại G. Chứng minh BD vuông góc CF và AE song song CF

c) Tia BD cắt CF tại G. chứng minh rằng D cách đều ba cạnh của tam giác AEG

d) lấy M và N tương ứng di động trên BF và bc sao cho BM + BN = BC. Chứng minh rằng trung điểm I của MN luôn nằm trên một đường thẳng cố định

Answer 1

[Trúc Giang]

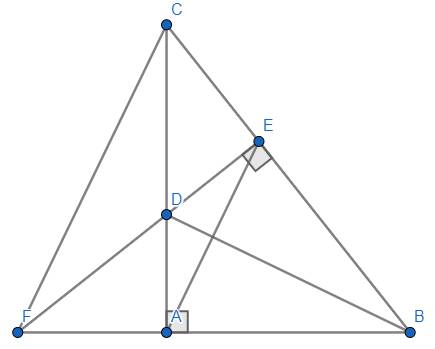
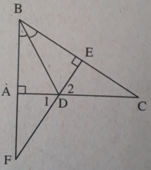
a/ Xét 2 tam giác vuông ΔABD và ΔEBD ta có:
Cạnh huyền BD: chung

\(\widehat{ABD}=\widehat{DBE}\left(GT\right)\)

=> ΔABD = ΔEBD (c.h - g.n)

=> AB = EB (2 cạnh tương ứng)

Gọi H là giao điểm của BD và AE

Xét ΔABH và ΔEBH ta có:

AB = EB (cmt)

\(\widehat{ABH}=\widehat{EBH}\left(GT\right)\)

BH: cạnh chung

=> ΔABH = ΔEBH (c - g - c)

=> AH = EH (2 cạnh tương ứng)

=> H là trung điểm của AE

=> BD đi qua trung điểm của AE (1)

Có: ΔABH = ΔEBH (cmt)

=> \(\widehat{AHB}=\widehat{EHB}\) (2 góc tương ứng)

Mà 2 góc này lại là 2 góc kề bù

\(\widehat{AHB}=\widehat{EHB}=180^0:2=90^0\)

=> AH ⊥ BH tại H

Hay: AE ⊥ BD tại H (2)

Từ (1) và (2) => BD là đường trung trực của AE

*Có: ΔABD = ΔEBD (cmt)

=> AD = DE (2 cạnh tương ứng) (3)

ΔDEC vuông tại E

=> DE là cạnh góc vuông

Và: DC là cạnh huyền

Mà cạnh huyền luôn > cạnh góc vuông

Nên: DC > DE (4)

Từ (3) và (4) => DC > AD

Hay: AD < DC

P/s: Câu b, c có liên quan đến điểm F mà điểm F lại ko đc nhắc đến trong đề nên mik ko làm đc nhé!