Một bếp điện (thứ 1) có R1 =20 ôm đặc vào một hiệu điện thế u không đổi , người ta đo đc 2 đầu bếp điện u= 100v . Thay bếp điện khác (thứ 2) có R2= 18ôm và u= 99v( mắc như trên)
Tính uAB ? Và diện trở dây dẫn r
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BA
B.Thị Anh Thơ
4 tháng 2 2020
https://i.imgur.com/2peeu8F.png
Đúng(0)
Những câu hỏi liên quan
N
15 tháng 11 2021
a. \(I=I1=I2=0,2A\left(R1ntR2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}U1=I1\cdot R1=0,2\cdot80=16V\\U2=U-U1=24-16=8V\end{matrix}\right.\)
\(\Rightarrow R2=U2:I2=8:0,2=40\Omega\)
b. \(R1nt\left(R2//R3\right)\)
\(I'=I1'=I23=0,27A\)
\(U23=U2=U3=U-U1'=24-\left(0,27\cdot80\right)=2,4V\)
\(I3=I23-I2=0,27-\left(2,4:40\right)=0,21A\)
\(\Rightarrow R3=U3:I3=2,4:0,21\approx11,4\Omega\)
VT
31 tháng 5 2018
Giải thích: Đáp án A
Phương pháp: Sử dụng hệ thức của định luật Ôm và công thức tính công suất tiêu thụ
Cách giải:
Giả sử cuộn dây thuần cảm:
Ta có, khi R = R2 công suất tiêu thụ trên biến trở cực đại.
Khi đó ta có: R2 = |ZL - ZC | = 40 - 25 = 15W
Mặt khác: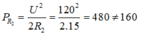 
=> điều giả sử ban đầu là sai
=> Cuộn dây không thuần cảm có điện trở r
- Ta có:
+ Ban đầu khi mắc vào hai đầu A, M một ắc quy có suất điện động E = 12V, điện trở trong r1 = 4W thì I1 = 0,1875
Theo định luật Ôm, ta có: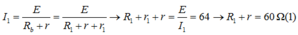 
+ Khi mắc vào A,B một hiệu điện thế u = 120 2 cos(100πt), R = R2 thì công suất tiêu thụ trên biến trở cực đại và bằng 160W
Ta có:
Công suất trên biến trở R đạt cực đại khi 
Mặt khác, ta có:
Công suất trên R2:
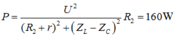
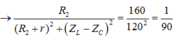
Kết hợp với (2) ta được: 
Với r = 20W thay vào (1) => R1 = 60 - 20 = 40W
VT
16 tháng 6 2018
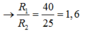
Đáp án A
Phương pháp: Sử dụng hệ thức của định luật Ôm và công thức tính công suất tiêu thụ
Cách giải:
Giả sử cuộn dây thuần cảm:
Ta có, khi R = R 2 công suất tiêu thụ trên biến trở cực đại
Khi đó ta có: R 2 = | Z L - Z C | = 40 - 25 = 15 W
Mặt khác: P R 2 = U 2 2 R 2 = 120 2 2.15 = 480 ≠ 160
⇒ điều giả sử ban đầu là sai
⇒ Cuộn dây không thuần cảm có điện trở r
- Ta có:
+ Ban đầu khi mắc vào hai đầu A, M một ắc quy có suất điện động E = 12V, điện trở trong r 1 = 4 W thì I 1 = 0 , 1875
Theo định luật Ôm, ta có: I 1 = E R b + r = E R 1 + r + r 1 → R 1 + r 1 + r = E I 1 = 64 → R 1 + r = 60 Ω ( 1 )
+ Khi mắc vào A,B một hiệu điện thế u = 120 2 cos 100 π t , R = R 2 thì công suất tiêu thụ trên biến trở cực đại và bằng 160W
Ta có:
Công suất trên biến trở R đạt cực đại khi R 2 2 = r 2 + Z L − Z C 2 ( 2 )
Mặt khác, ta có:
Công suất trên R 2 : P = U 2 ( R 2 + r ) 2 + Z L − Z C 2 R 2 = 160 W → R 2 ( R 2 + r ) 2 + Z L − Z C 2 = 160 120 2 = 1 90
90 R 2 = 2 R 2 2 + 2 r R → R 2 + r = 45
Kết hợp với (2) ta được: R 2 2 = ( 45 − R 2 ) 2 + 15 2 → R 2 = 25 Ω , r = 20 Ω
Với r = 20W thay vào (1) ⇒ R 1 = 60 - 20 = 40 Ω
→ R 1 R 2 = 40 25 = 1,6
HD
Hà Đức Thọ
Admin
17 tháng 12 2015
\(Z_L=\omega L=100\sqrt{3}\Omega\)
C thay đổi để Uc max khi: \(Z_C=\frac{R^2+Z_L^2}{Z_L}=\frac{100^2+3.100^2}{100\sqrt{3}}=\frac{4}{\sqrt{3}}.100\Omega\)
\(U_{cmax}=U\frac{\sqrt{R^2+Z_L^2}}{R}=100\frac{\sqrt{100^2+3.100^2}}{100}=200V\)
VT
22 tháng 1 2019
Đáp án D
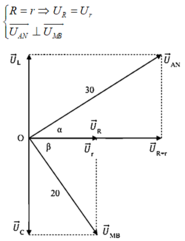
Phương pháp: Sử dụng giản đồ vecto
Cách giải:
Dựa vào đồ thị và dữ kiện đề bài:
N
7 tháng 12 2021
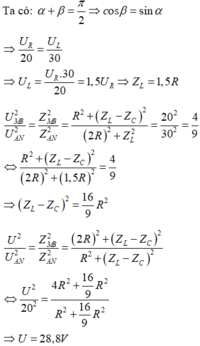
a. \(R=\dfrac{U^2}{P}=\dfrac{220^2}{1000}=48,4\Omega\)
b. \(H=\dfrac{Q_{thu}}{Q_{toa}}100\%=\dfrac{mc\Delta t}{Pt}100\%=\dfrac{2,5\cdot4200\cdot80}{1000\cdot15\cdot60}100\%\approx93,3\%\)
c. \(R=p\dfrac{l}{S}=>l=\dfrac{R\cdot S}{p}=\dfrac{48,4\cdot0,02\cdot10^{-6}}{0,4\cdot10^{-6}}=2,42\left(m\right)\)
d. Theo PTCBN: \(Q'=2Q_{thu}=2\cdot\left(2,5\cdot4200\cdot80\right)=1680000\left(J\right)\approx0,5\)kWh
\(=>T=Q'\cdot1500=0,5\cdot30\cdot1500=22500\left(dong\right)\)
Câu cuối mình không chắc lắm nhé >_<
có là dc r :>
N
6 tháng 11 2021
a. \(R=\dfrac{U^2}{P}=\dfrac{220^2}{1000}=48,4\Omega\)
b. \(H=\dfrac{Q_{nc}}{Q_{tp}}100\%=\dfrac{mc\left(t-t_1\right)}{Pt}100\%=\dfrac{2,5.4200\left(100-20\right)}{1000.15.60}100\%=93,3\%\)c. \(R=p\dfrac{l}{S}\Rightarrow l=\dfrac{R.S}{p}=\dfrac{48,4.0,02.10^{-6}}{0,4.10^{-6}}=2,42\left(m\right)\)
d. \(Q'=\dfrac{2Q}{H}=\dfrac{2.840000}{0,93}=1806451,613\left(J\right)\)
\(\Rightarrow Q_{tp}=Q'.30=1806451,613.30=54193548,39\left(J\right)=15,1\)kWh
\(\Rightarrow T=Q_{tp}1500=15,1.1500=22650\left(dong\right)\)