cho tam giác ABC có BC=15cm,đường cao AH=10cm.Một đường thẳng d song song với BC và cắt các cạnh AB và AC theo thứ tự ở D và E
a) Tính SABC
b) Tính DE nếu khoảng cách từ d đến BC bằng 4cm
c) Tính DE nếu DE bằng khoảng cách từ d đến BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LV
11 tháng 2 2020
Dựa vào tính chất đường trung bình của tam giác:
DM=EN/2
theo tính chất đương trung bình của hình thang:
EN=(DM+m)/2
CM
6 tháng 2 2018
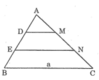
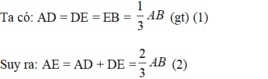
Trong ΔABC, ta có: DM // BC (gt)
Nên 
(Hệ quả định lí Ta-lét)
Suy ra : 
(3)
Từ (1) và (3) suy ra: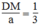 
Suy ra: 
Trong ΔABC, ta có: EN // BC (gt)
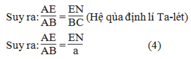
Từ (2) và (4) suy ra: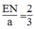 
hay 
KT
10 tháng 3 2021
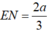
Mình cx ko bik nx tại vì này là thầy mình chụp bài của bên trường gửi qua lớp mình á, này là thầy mình gửi qua á
PA
23 tháng 12 2016
ABD = EDC (2 góc đồng vị, AB // DE)
mà ABD = ECD (tam giác ABC cân tại A)
=> EDC = ECD
=> Tam giác ECD cân tại E
=> ED = EC
Xét tam giác AFE và tam giác DEF có:
AFE = DEF (2 góc so le trong, AF // DE)
FE chung
FEA = EFD (2 góc so le trong, EA // FD)
=> Tam giác AFE = Tam giác DEF (g.c.g)
=> AE = DF (2 cạnh tương ứng)
mà ED = EC (chứng minh trên)
=> DF + ED = AE + EC = AC = 3 (cm)
31 tháng 12 2022
Xét ΔAEF và ΔDFE có
góc AEF=góc DFE
EF chung
góc AFE=góc DEF
Do đó: ΔAEF=ΔDFE
Xét ΔEDC có góc EDC=góc ECD
nên ΔEDC cân tại E
=>ED=CE=3-AE
Xét ΔFBD có góc FDB=góc FBD
nên ΔFBD cân tại F
=>FD=FB=3-AF=3-DE=3-EC
ED+FD=3-AE+3-DE=3-AE+3-EC=6-3=3cm