Cho tam giác ABC. Kẻ AD là toán phân giác của góc BAC( D thuộc BC). Từ D vẽ một đường thẳng vuông góc với BC cắt AC tại M. Tính số đo góc MBC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
10 tháng 1 2017
Gọi O là giao điểm của CM và AD; I là giao điểm của CN và BE.
Do AD là tia phân giác góc A nên ta thấy ngay \(\Delta ACD=\Delta AMD\) (Cạnh huyền góc nhọn)
Vậy thì AC = AM; DC = DM hay AD là trung trực của CM. Vậy nên \(\widehat{COD}=90^o.\)
Từ đó ta có \(\widehat{OCD}+\widehat{CDO}=90^o\) mà \(\widehat{CAD}+\widehat{CDO}=90^o\Rightarrow\widehat{OCD}=\widehat{CAD}=\frac{\widehat{CAB}}{2}\)
Hoàn toàn tương tự \(\widehat{ACN}=\frac{\widehat{ABC}}{2}\)
Ta có \(\widehat{ABC}+\widehat{BAC}=90^o\Rightarrow2\widehat{ACN}+2\widehat{BCM}=90^o\)
\(\Rightarrow\widehat{ACN}+\widehat{BCM}=45^o\Rightarrow\widehat{MCN}=90^o-45^o=45^o.\)
19 tháng 5 2022
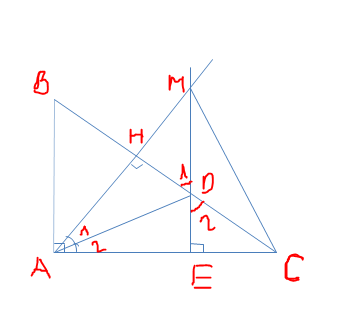
a/ Xét \(\Delta\) vuông AHD và \(\Delta\) AED. Có:
\(\widehat{A1}\)= \(\widehat{A2}\) ( giả thiết)
AD chung
=> \(\Delta AHD=\Delta AED\) ( ch-gn)
=> DH = DE ( 2 cạnh tương ứng )
b/ BMC không cân được bạn nhé. bạn chép nhầm đề bài r: Chứng minh DMC cân mới đúng.
Xét \(\Delta vuôngHDM\) và \(\Delta vuôngEDC\). Có:
\(\widehat{D1}\) = \(\widehat{D2}\) ( đối đỉnh)
HD = HE ( cmt)
=> \(\Delta HDM=\Delta EDC\left(cgv-gnk\right)\)
=> DM = DC ( 2 cạnh tương ứng)
=> Xét \(\Delta DMCcóDM=DC=>\Delta DMCcân\left(cântạiD\right)\)
~ Cậu ktra lại nhé~
12 tháng 1
a: Ta có:ΔABC vuông tại B
=>\(\widehat{BAC}+\widehat{BCA}=90^0\)
=>\(\widehat{BAC}+50^0=90^0\)
=>\(\widehat{BAC}=40^0\)
b: Xét ΔABE và ΔADE có
AB=AD
\(\widehat{BAE}=\widehat{DAE}\)
AE chung
Do đó: ΔABE=ΔADE
c: Xét ΔFAB vuông tại A và ΔEBA vuông tại B có
AB chung
\(\widehat{FBA}=\widehat{EAB}\)(hai góc so le trong, FB//AE)
Do đó: ΔFAB=ΔEBA
d: Sửa đề: I là trung điểm của BA
Xét tứ giác AFBE có
AF//BE
AE//BF
Do đó: AFBE là hình bình hành
=>AB cắt FE tại trung điểm của mỗi đường
mà I là trung điểm của AB
nên I là trung điểm của FE
=>F,I,E thẳng hàng
29 tháng 1 2018
âu trả lời hay nhất: xét tứ giác ABDM
có ^A=90 o ( tam giác ABC vuông tại A theo gt )
^D = 90 o ( gt )
=> ^A + ^D = 180 o
=> t/g ABDM là t/g nội tiếp ( dhnb )
=> góc BAD = góc BMD ( góo nội tiếp cùng chắn cung BD )
lại có ^ BAD = 1/2 ^ BAC = 1/2 90 o = 45 o
=> ^BMD = 45 o
p/s : kham khảo