Cho tam giác ABC nội tiếp (O). Gọi D là điểm thuộc cung AB. Qua D kẻ dây DD' // BC ở F. Đường thẳng AD' cắt BC ở E.
a, CMR:ΔABD∼ΔAEC và ΔABE∼ΔADC.
b,CMR: AD.AE=AB.AC
c,CMR: ΔAFD∼ΔAD'B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

DE//AB
=>sđ cung AD=sđ cung BE=sđ cung CD=1/2*sđ cung AC
góc BIE=1/2(sđ cung BE+sđ cung CD)
=1/2*(sđ cung CD+sđ cung CD)
=sđ cung CD
=2*góc CEI
=>ΔIEC cân tại I
=>IE=IC
Xét ΔIBE và ΔIDC có
góc BIE=góc DIC
IE=IC
góc IEB=góc ICD
=>ΔIBE=ΔIDC
=>IB=ID
=>ΔIBD cân tại I

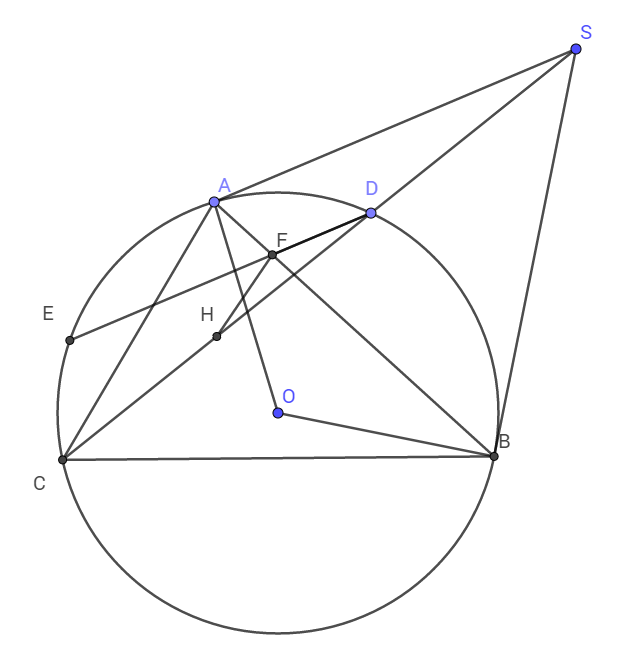
Ta có các tam giác vuông AOS; HOS, BOS có chung cạnh huyền OS nên S, A, H, O, B nội tiếp đường tròn đường kính OS.
Khi đó ta có :
\(\widehat{ASH}=\widehat{ABH}\) (Hai góc nội tiếp cùng chắn cung AH)
Mà \(\widehat{ASH}=\widehat{FDH}\) (Hai góc đồng vị)
\(\Rightarrow\widehat{ABH}=\widehat{FDH}\)
Suy ra tứ giác HFDO nội tiếp.
Từ đó ta có \(\widehat{FHD}=\widehat{ABD}\)(Hai góc nội tiếp)
Mà \(\widehat{ABD}=\widehat{ACD}\) (Hai góc nội tiếp)
Nên \(\widehat{FHD}=\widehat{ACD}\)
Chúng lại ở vị trí đồng vị nên HF // AC.
@Akai Haruma help me
DD'//BC ở F???