Cho x,y,z đôi một khác nhau thỏa mãn
x3(y - z) + z3(x - y) = y3(z - x).
CMR: x3 + y3 + z3 = 3xyz
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng bđt AM - GM:
\(x^3+1+1\ge3x;y^3+1+1\ge3y;z^3+1+1\ge3z;2x+2y+2z\ge6\sqrt[3]{xyz}=6\).
Cộng vế với vế các bđt trên rồi rút gọn ta có đpcm.

\(x^3+y^3+z^3-3xyz=0\)
\(\Leftrightarrow\left(x+y\right)^3+z^3-3xy\left(x+y\right)-3xyz=0\)
\(\Leftrightarrow\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2-3xy\right)=0\)
\(\Leftrightarrow x^2+y^2+z^2-xy-xz-yz=0\)
\(\Leftrightarrow x=y=z\)

Bài 3:
a, (\(x\)+y+z)2
=((\(x\)+y) +z)2
= (\(x\) + y)2 + 2(\(x\) + y)z + z2
= \(x^2\) + 2\(xy\) + y2 + 2\(xz\) + 2yz + z2
=\(x^2\) + y2 + z2 + 2\(xy\) + 2\(xz\) + 2yz
b, (\(x-y\))(\(x^2\) + y2 + z2 - \(xy\) - yz - \(xz\))
= \(x^3\) + \(xy^2\) + \(xz^2\) - \(x^2\)y - \(xyz\) - \(x^2\)z - y3
Đến dây ta thấy xuất hiện \(x^3\) - y3 khác với đề bài, em xem lại đề bài nhé

Ta rút gọn tử thức trc: \(x^3+y^3+z^3-3xyz=x^3+y^3+z^3+x^2y-x^2y+xy^2-xy^2+y^2z-y^2z+yz^2-yz^2+x^2z-x^2z+xz^2-xz^2-xyz-xyz-xyz=x^2\left(x+y+z\right)+y^2\left(x+y+z\right)+z^2\left(x+y+z\right)-x\left(x+y+z\right)-yz\left(x+y+z\right)-xz\left(x+y+z\right)=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)=\frac{1}{2}\left(x+y+z\right)\left(x^2-2xy+y^2+y^2-2yz+z^2+z^2-2xz+x^2\right)=\frac{1}{2}\left(x+y+z\right)\left(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right)\)tới đây rút gọn đc rồi chứ

Lời giải:
\(A=\frac{x^3-y^3-z^3-3xyz}{(x+y)^2+(y-z)^2+(x+z)^2}=\frac{(x-y)^3+3xy(x-y)-z^3-3xyz}{x^2+y^2+2xy+y^2-2yz+z^2+z^2+x^2+2xz}\)
\(=\frac{(x-y)^3-z^3+3xy(x-y-z)}{2x^2+2y^2+2z^2+2xy-2yz+2xz}=\frac{(x-y-z)[(x-y)^2+z(x-y)+z^2]+3xy(x-y-z)}{2(x^2+y^2+xy-yz+xz)}\)
\(=\frac{(x-y-z)[(x-y)^2+z(x-y)+z^2+3xy]}{2(x^2+y^2+xy-yz+xz)}=\frac{(x-y-z)(x^2+y^2+z^2+xy-yz+xz)}{2(x^2+y^2+z^2+xy-yz+xz)}=\frac{x-y-z}{2}\)

Ta có: \(x^3+y^3+z^3-3xyz\)
\(=\left(x+y\right)^3-3xy\left(x+y\right)+z^3-3xyz\)
\(=\left[\left(x+y\right)^3+z^3\right]-\left[3xy\left(x+y\right)+3xyz\right]\)
\(=\left(x+y+z\right)\left[\left(x+y\right)^2-z\left(x+y\right)+z^2\right]-\left[3xy\left(x+y+z\right)\right]\)
\(=\left(x+y+z\right)\left(x^2+2xy+y^2-zx-zy+z^2\right)-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(x^2+2xy+y^2-zx-zy+z^2-3xy\right)\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)\)(đpcm)

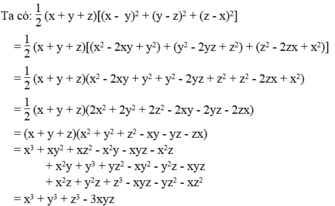
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu x ≥ 0, y ≥ 0, z ≥ 0 thì:
x + y + z ≥ 0
x - y 2 + y - z 2 + z - x 2 ≥ 0
Suy ra:
x 3 + y 3 + z 3 - 3 x y z ≥ 0 ⇔ x 3 + y 3 + z 3 ≥ 3 x y z
Hay: x 3 + y 3 + z 3 3 ≥ x y z

Ta có: \(x^3-y^3=3x-3y\Leftrightarrow x^2+xy+y^2=3\) (Do \(x\neq y\)).
Tương tự: \(y^2+yz+z^2=3;z^2+zx+x^2=3\).
Cộng vế với vế ta có: \(2\left(x^2+y^2+z^2\right)+xy+yz+zx=9\)
\(\Leftrightarrow\dfrac{3\left(x^2+y^2+z^2\right)}{2}+\dfrac{\left(x+y+z\right)^2}{2}=9\).
Mặt khác, từ đó ta cũng có: \(\left(x^2+xy+y^2\right)-\left(y^2+yz+z^2\right)=0\Leftrightarrow\left(x+y+z\right)\left(x-z\right)=0\Leftrightarrow x+y+z=0\).
Do đó \(x^2+y^2+z^2=6\left(đpcm\right)\).

a: Ta có: \(\left(x+y\right)^2\)
\(=x^2+2xy+y^2\)
\(\Leftrightarrow x^2+y^2=\dfrac{\left(x+y\right)^2}{2xy}\ge\dfrac{\left(x+y\right)^2}{2}\forall x,y>0\)