Cho tứ giác ABCD,gọi M,N lần lượt là trung điểm các cạnh BC và CD.CMR SABCD < 1/2(AM+AN)2
GIÚP MK VS
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương pháp:
Công thức tính thể tích khối chóp có diện tích đáy S và chiều cao h là: V = 1 3 S h
Cách giải:
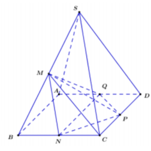
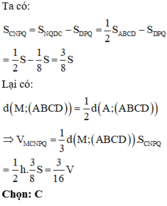

a: Gọi E là trung điểm của AB
ΔABC đều nên CE vuông góc AB
ΔABD đều nên DE vuông góc AB
=>AB vuông góc (CDE)
=>AB vuông góc CD
b: Xét ΔCAB có CN/CB=CM/CA
nên MN//AB và MN=1/2AB
Xét ΔDAB có DQ/DA=DP/DB
nên PQ//AB và PQ/AB=DQ/DA=1/2
=>MN//PQ và MN=PQ
=>MNPQ là hình bình hành
Xét ΔADC có AQ/AD=AM/AC
nên QM//DC
=>QM vuông góc AB
=>QM vuông góc QP
=>MNPQ là hình chữ nhật

Gọi K là trung điểm BD
Xét tam giác ABD có:
Mlà trung điểm AD
K là trung điểm BD
=> MK là đường trung bình
\(\Rightarrow MK=\dfrac{1}{2}AB\left(1\right)\)
Xét tam giác BDC có:
K là trung điểm BD
N là trung điểm BC
=> NK là đường trung bình
\(\Rightarrow NK=\dfrac{1}{2}DC\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow MK+NK=\dfrac{1}{2}\left(BC+DC\right)\)
Mà \(MK+NK\ge MN\)(bất đẳng thức trong tam giác KMN)
\(\Rightarrow MN\le\dfrac{AB+DC}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow MK+NK=MN\)
\(\Leftrightarrow\) K là trung điểm MN