Tìm giá trị nhỏ nhất của biểu thức:
\(B=x^2-2xy+2y^2+2x-4y-2015\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BC
1
TT
25 tháng 12 2020
\(A=x^2+2x\left(y+1\right)+\left(y+1\right)^2-\left(y+1\right)^2+2y^2-4y+2028\)
\(=\left(x+y+1\right)^2-y^2-2x-1+2y^2-4y+2028\)
\(=\left(x+y+1\right)^2-6x+y^2+2027\)
\(=\left(x+y+1\right)+\left(y-3\right)^2+2018\ge2018\forall x;y\) (do...)
=> MinA = 2018 \(\Leftrightarrow\left\{{}\begin{matrix}x+y=-1\\y=3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=3\end{matrix}\right.\)
PB
3
TM
9 tháng 7 2017
\(Q=x^2+2y^2+2xy-2x-6y+2015\)
\(Q=x^2+2x\left(y-1\right)+2y^2-6y+2015\)
\(Q=x^2+2x\left(y-1\right)+y^2-2y+1+y^2-4y+4+2010\)
\(Q=x^2+2x\left(y-1\right)+\left(y-1\right)^2+\left(y-2\right)^2+2010\)
\(Q=\left(x+y-1\right)^2+\left(y-2\right)^2+2010\ge2010\forall x;y\)
Dấu "=" xảy ra khi x=-3;y=4
BC
1
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 12 2020
\(A=\left(x^2+y^2+1+2xy+2x+2y\right)+\left(y^2-6y+9\right)+2018\)
\(A=\left(x+y+1\right)^2+\left(y-3\right)^2+2018\ge2018\)
\(A_{min}=2018\) khi \(\left\{{}\begin{matrix}x=-4\\y=3\end{matrix}\right.\)
BC
25 tháng 12 2020
Giúp mk bài hình mk mới đăng với Nguyễn Việt Lâm Quản lý, ý b,c, d thôi
NQ
0
NC
2
7 tháng 4 2015
\(A=x^2+2xy+2y^2+2x-4y+2013\)
\(=\left(x^2+y^2+1+2x+2y+2xy\right)-1-2y+y^2-4y+2013\)\(=\left(x+y+1\right)^2+\left(y^2-2.y.3+9\right)-9+2012\)
\(=\left(x+y+1\right)^2+\left(y-3\right)^2+2003\)
mà \(\left(x+y+1\right)^2,\left(y-3\right)^2\ge0\)
\(\Rightarrow A=x^2+2xy+2y^2+2x-4y+2013=\left(x+y+1\right)^2+\left(y-3\right)^2+2003\ge2003\)
\(\Rightarrow Min\left(A\right)=2003\)
5 tháng 2 2022
b: Tham khảo:
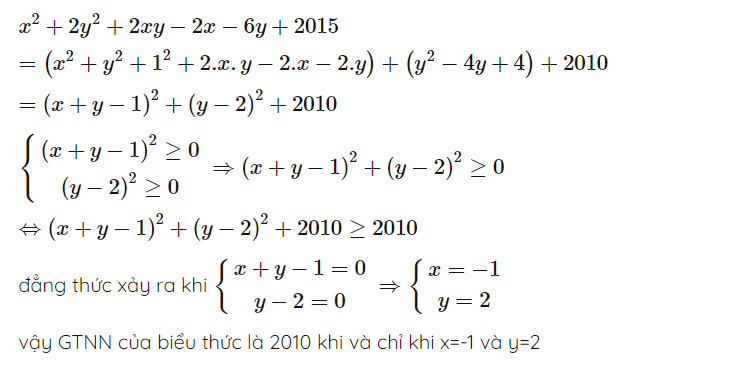
a: \(P=x^2-5x+\dfrac{25}{4}-\dfrac{25}{4}=\left(x-\dfrac{5}{2}\right)^2-\dfrac{25}{4}\ge-\dfrac{25}{4}\forall x\)
Dấu '=' xảy ra khi x=5/2
SA
3
NC
19 tháng 8 2020
Bài làm:
a) \(P=x^2-5x=\left(x^2-5x+\frac{25}{4}\right)-\frac{25}{4}\)
\(=\left(x-\frac{5}{2}\right)^2-\frac{25}{4}\le-\frac{25}{4}\left(\forall x\right)\)
Dấu "=" xảy ra khi: \(x=\frac{5}{2}\)
Vậy \(Min_P=-\frac{25}{4}\Leftrightarrow x=\frac{5}{2}\)
19 tháng 8 2020
a) P = x2 - 5x
= ( x2 - 5x + 25/4 ) - 25/4
= ( x - 5/2 )2 - 25/4
( x - 5/2 )2 ≥ 0 ∀ x => ( x - 5/2 )2 - 25/4 ≥ -25/4
Đẳng thức xảy ra <=> x - 5/2 = 0 => x = 5/2
=> MinF = -25/4 <=> x = 5/2
b) Q = x2 + 2y2 + 2xy - 2x - 6y + 2015
= ( x2 + 2xy + y2 - 2x - 2y + 1 ) + ( y2 - 4y + 4 ) + 2010
= [ ( x + y )2 - 2( x + y ) + 12 ] + ( y - 2 )2 + 2010
= ( x + y - 1 )2 + ( y - 2 )2 + 2010
\(\hept{\begin{cases}\left(x+y-1\right)^2\ge0\forall x,y\\\left(y-2\right)^2\ge0\forall x\end{cases}}\Rightarrow\left(x+y-1\right)^2+\left(y-2\right)^2+2010\ge2010\)
Đẳng thức xảy ra <=> \(\hept{\begin{cases}x+y-1=0\\y-2=0\end{cases}}\Rightarrow\hept{\begin{cases}x+y-1=0\\y=2\end{cases}}\Rightarrow\hept{\begin{cases}x=-1\\y=2\end{cases}}\)
=> MinQ = 2010 <=> x = -1 , y = 2
OK
0
biet tong cua so thu nhat va so thu hai bang 5,8.Tong cua so thu hai va so thu ba bang 6,7.Tong so thu nhat va so thu ba bang 7,5.Tim moi so do?