Bài 3. Tìm k để 3 điểm sau thẳng hàng M ( 2; -1), N (1; 1 ) và P ( 3; k + 1).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tìm k để 3 điểm sau thẳng hàng M ( 2; -1), N (1; 1 ) và P ( 3; k + 1).
Gọi phương trình đường thẳng đi qua 2 điểm M, N là y = ax + b
Khi đó ta có:
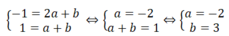
Phương trình đường thẳng MN là: y = - 2x + 3
Để 3 điểm M, N, P thẳng hàng thì P nằm trên đường thẳng MN
⇔ k + 1 = -2.3 + 3 ⇔ k + 1 = -3 ⇔ k = -4 (Thỏa mãn ĐK)


a: Thay x=0 và y=0 vào (1), ta được:
k=0
c: Để (1)//\(y=\left(\sqrt{3}+1\right)x+3\), ta được:
\(\left\{{}\begin{matrix}k+1=\sqrt{3}+1\\k\ne3\end{matrix}\right.\Leftrightarrow k=\sqrt{3}\)