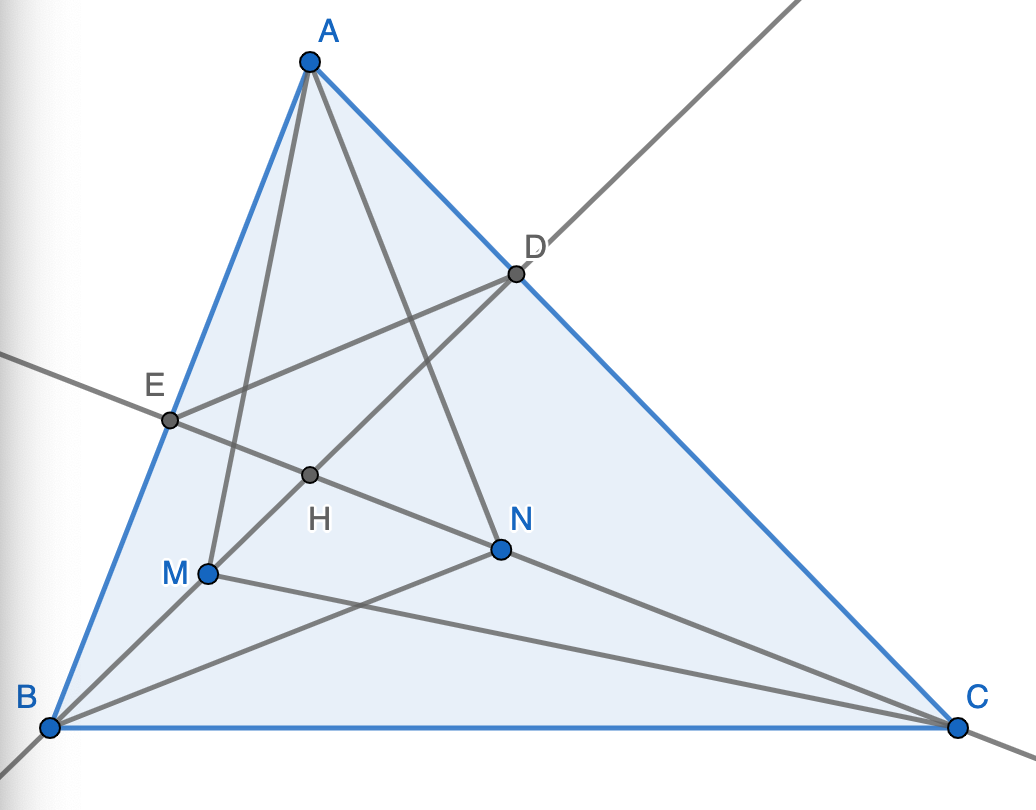
Cho ngũ giác ABCDE sao cho \(\widehat{B}=\widehat{E}=90\)và \(\widehat{EAD}=\widehat{BAC}\)BD cắt CE tại O
CMR \(AO\perp BE\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trên cạnh BA của \(\Delta\)ABC lấy điểm G sao cho BG = BC. Ta có:
^CFB = 1800 - ^BCF - ^CBF = 1800 - ^BCE - ^CBE = 700 => ^CFB = ^BCF (=700)
=> \(\Delta\)CBF cân tại B => BF = BC = BG => \(\Delta\)GBF cân tại B => ^BGF = (1800 - ^GBF)/2 = 800
=> ^FGA = 1000. Gọi GF cắt AC tại L. Trên đoạn GL lấy điểm F' sao cho ^CAF' = 100
Qua F' dựng đường thẳng song song với AB, đường thẳng này cắt AC tại H
Trên nửa mặt phẳng bờ AB có chứa điểm C, dựng \(\Delta\)GAK đều
Xét \(\Delta\)ALG: ^LGA = 1000 (cmt), ^LAG = 400 => \(\Delta\)ALG cân tại G => \(\Delta\)LF'H cân tại F' (F'H // AG)
Xét \(\Delta\)CLG: ^GCL = ^ACB - ^BCG = 200, ^CLG = 1800 - ^GLA = 1400 => \(\Delta\)CLG cân tại L
Có ^GAF' = ^BAC - ^CAF' = 300 = ^GAK/2 => ^GAF' = ^KAF'. Từ đây dễ có \(\Delta\)F'GA = \(\Delta\)F'KA (c.g.c)
=> F'G = F'K => \(\Delta\)GF'K cân tại F'. Do ^F'GK = ^F'GA - ^KGA = 400 nên ^GF'K = 1000
Suy ra ^GF'K = ^HF'L (= ^AGL = 1000) => ^GF'H = ^KF'L (= 1000 - ^KF'H)
Kết hợp với F'H = F'L; F'G = F'K (cmt) suy ra \(\Delta\)HF'G = \(\Delta\)LF'K (c.g.c) => ^F'LK = ^F'HG
Dễ dàng tính được ^F'LK = ^GLK = (1800 - 400)/2 = 700 => ^F'HG = 700 => ^HGA = 700 (Vì F'H // AG)
Ta thấy \(\Delta\)AGH có ^GAH = 400 , ^HGA = 700 => \(\Delta\)AGH cân tại A
Từ đó AH = AG = GL = CL (Vì các tam giác AGL, CLG cân). Dễ dàng chứng minh:
\(\Delta\)CLF' = \(\Delta\)AHF' (c.g.c) (F'L = F'H, ^F'LC = ^F'HA, CL = AH) => ^LCF' = ^HAF' = ^CAF' = 100
=> ^BCF' = 700 = ^BCE => CF' trùng CE. Ban đầu ta nhận thấy CE cắt GL tại F
Mà CF' trùng CE, F' thuộc GL nên F' trùng F. Tức là ^CAF = ^CAF' = 100 => ^CAF + ACB = 900
Vậy thì AF vuông góc với BC (đpcm).

Bổ sug đề: Cho (O), BD,CE là các dây của (O)
Sửa đề: Chứng minh góc BOE=góc EDB+góc ECB
1/2(góc EDB+góc ECB)
=1/2(1/2sđ cung EB+1/2sđ cung EB)
=1/2sđ cung EB
=1/2*góc BOE
=>góc EDB+góc ECB=góc BOE

nhanh lên mình cần gấp lắm
giúp mình với huhuhuhuhuhuhuhuhuhuhuhuhuhuhuhuhuhu
Cho tam giác ABC, phân giác BD, CE cắt nhau tại I. Biết BD.CE = 2.BI.CI. CMR: \(\widehat{BAC=90^o}\)

Ta có bài toán phụ sau: Nếu \(\frac{a}{b}=\frac{c}{d}\) thì \(\frac{a}{a+b}=\frac{c}{c+d}\)
Chứng minh:
\(\frac{a}{b}=\frac{c}{d}\Rightarrow ad=bc\Leftrightarrow ac+ad=ac+bc\Leftrightarrow a\left(c+d\right)=c\left(a+b\right)\Rightarrow\frac{a}{a+b}=\frac{c}{c+d}\)
Áp dụng vào bài toán:
Theo t/c đường phân giác trong tam giác, ta có: \(\frac{CD}{AD}=\frac{BC}{AB}\)
\(\Rightarrow\frac{CD}{CD+AD}=\frac{BC}{BC+AB}\Rightarrow\frac{CD}{AC}=\frac{BC}{AB+BC}\Rightarrow CD=\frac{BC.AC}{AB+BC}\)(1)
Tương tự: \(BE=\frac{BC.AB}{BC+AC}\)(2)
Trong tam giác DBC có phân giác CI nên \(\frac{BI}{DI}=\frac{BC}{CD}\Rightarrow\frac{BI}{DI+BI}=\frac{BC}{CD+BC}\)(3)
Thế (1) vào (3), được
\(\Rightarrow\frac{BI}{BD}=\frac{BC}{BC+\frac{BC.AC}{AB+BC}}=\frac{BC}{\frac{BC.\left(AB+AC+BC\right)}{AB+BC}}=\frac{AB+BC}{AB+AC+BC}\)(*)
Lại có: \(\frac{CI}{EI}=\frac{BC}{BE}\Rightarrow\frac{CI}{CE}=\frac{BC}{BC+BE}\)(4)
Thế (2) vào (4) \(\Rightarrow\frac{CI}{CE}=\frac{BC}{BC+\frac{BC.AB}{BC+AC}}=\frac{BC}{\frac{BC\left(AB+AC+BC\right)}{BC+AC}}=\frac{BC+AC}{AB+AC+BC}\)(2*)
Nhân (*) với (2*) \(\Rightarrow\frac{BI.CI}{BD.CE}=\frac{\left(AB+BC\right)\left(BC+AC\right)}{\left(AB+AC+BC\right)^2}\).
Mà \(BD.CE=2.BI.CI\Rightarrow\frac{\left(AB+BC\right)\left(AC+BC\right)}{\left(AB+AC+BC\right)^2}=\frac{1}{2}\)
\(\Rightarrow2.\left(BC^2+AB.BC+AC.AB+AC.BC\right)=AB^2+AC^2+BC^2+2.\left(AB.BC+AC.AB+AC.BC\right)\)\(\Leftrightarrow2BC^2=AB^2+AC^2+BC^2\Leftrightarrow BC^2=AB^2+AC^2\)
Suy ra tam giác ABC vuông tại A (ĐL Pytago đảo). Hay ^BAC = 900 (đpcm).

Câu hỏi của giang ho dai ca - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại link trên nhé.