Giúp mình với mọi người ơi huhu

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 5:
4: ta có: \(5x\left(-x+1\right)-5\left(-x^2-x\right)=0\)
\(\Leftrightarrow-5x\left(x-1\right)+5x\left(x+1\right)=0\)
\(\Leftrightarrow5x\left(-x+1+x+1\right)=0\)
hay x=0

Bài 15:
\(a,ĐK:y>0;y\ne1\\ b,Q=\left[\dfrac{\sqrt{y}\left(\sqrt{y}-1\right)}{\sqrt{y}-1}-\dfrac{\sqrt{y}+1}{\sqrt{y}\left(\sqrt{y}+1\right)}\right]\cdot\dfrac{y}{\sqrt{y}+1}\\ Q=\left(\sqrt{y}-\dfrac{1}{\sqrt{y}}\right)\cdot\dfrac{y}{\sqrt{y}+1}=\dfrac{y-1}{\sqrt{y}}\cdot\dfrac{y}{\sqrt{y}+1}\\ Q=\sqrt{y}\left(\sqrt{y}-1\right)\\ c,Q=y-\sqrt{y}+\dfrac{1}{4}-\dfrac{1}{4}=\left(\sqrt{y}-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\\ Q_{min}=-\dfrac{1}{4}\Leftrightarrow\sqrt{y}=\dfrac{1}{2}\Leftrightarrow y=\dfrac{1}{4}\left(tm\right)\)

\(C=\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)-\sqrt{x}\left(\sqrt{x}+2\right)+6\sqrt{x}}{x-4}.\left(x-4\right)=2\sqrt{x}\)

Bài 5 :
a, \(x+3=1\Leftrightarrow x=-2\)
b, \(19-x=-61\Leftrightarrow x=80\)
c, \(21-7x-12x+60=5\Leftrightarrow-19x=-76\Leftrightarrow x=4\)
d, \(\left(x-3\right)\left(x^2+1>0\right)=0\Leftrightarrow x=3\)

1: Để C là số nguyên thì 2n+2-3 chia hết cho n+1
=>\(n+1\in\left\{1;-1;3;-3\right\}\)
=>\(n\in\left\{0;-2;2;-4\right\}\)

b) Ta có: ΔDBC vuông tại B(gt)
nên \(\widehat{D}+\widehat{C}=90^0\)(hai góc nhọn phụ nhau)(1)
Ta có: \(\widehat{ABD}+\widehat{ABC}=\widehat{DBC}\)(BA là tia nẵm giữa hai tia BD,BC)
nên \(\widehat{ABD}+\widehat{ABC}=90^0\)(2)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\widehat{C}\)(hai góc ở đáy)(3)
Từ (1), (2) và (3) suy ra \(\widehat{ABD}=\widehat{ADB}\)
Xét ΔABD có \(\widehat{ABD}=\widehat{ADB}\)(cmt)
nên ΔABD cân tại A(Định lí đảo của tam giác cân)
a) Xét ΔAMB và ΔAMC có
AM chung
AB=AC(ΔABC cân tại A)
MB=MC(M là trung điểm của BC)
Do đó: ΔAMB=ΔAMC(c-c-c)






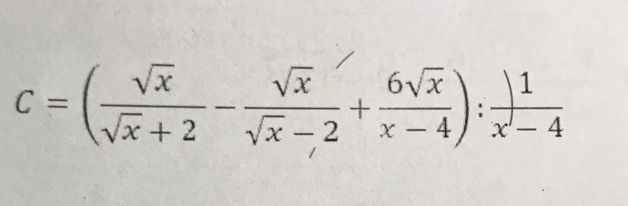
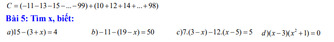 mọi người ơi, giúp em với sắp thi roii huhu
mọi người ơi, giúp em với sắp thi roii huhu

a) \(R_2=\rho\dfrac{l}{S}=2,8.10^{-8}.\dfrac{2,10^{-3}}{10.10^{-6}}=5,6.10^{-6}\left(\Omega\right)\)
b) Điện trở tương đương:
\(R_{tđ}=R_1+R_2=5,6.10^{-6}+20\approx20\left(\Omega\right)\)
Điện trở R2: \(R_2=p\dfrac{l}{S}=2,8.10^{-8}\dfrac{0,002}{10.10^{-6}}=5,6.10^{-6}\Omega\)
Điện trở tương đương: \(R=R1+R2=20+5,6.10^{-6}\simeq20\Omega\)