Bài 1 : Cho hình vuông ABCD có E ,F là TĐ AB ,ACa) CM: CE vuông với DFb) Gọi DF cắt CE tại M . CM AM = AB Bài 2:Cho hình vuông ABCD . Qua M thuộc đường chéo AC , Kẻ ME vuông với AD

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

A

anhmiing

14 tháng 11 2019 - olm

Bài 1 : Cho hình vuông ABCD có E ,F là TĐ AB ,AC

a) CM: CE vuông với DF

b) Gọi DF cắt CE tại M . CM AM = AB

Bài 2:Cho hình vuông ABCD . Qua M thuộc đường chéo AC , Kẻ ME vuông với AD ; MF vuông CD . CMR:

a) BE vuông với AF

b) BM vuông với EF

1

A

anhmiing

14 tháng 11 2019

c) BM , AF , CE đồng quy

Những câu hỏi liên quan

NL

Ngô Linh

19 tháng 11 2017 - olm

Bài 3: Hình vuông ABCD. E thuộc AB: EA=EB, F thuộc CB: FC=FB. CMR:a) CE vuông góc với DFb) CE cắt DF tại M. CMR: AM=ADBài 4: Hình vuông ABCD, AB=BC=CD=DA=4cm. I là trung điểm của AD, E đối xứng với A qua BI, BE cắt CD ở F. Tính DF=?Bài 5: Hình vuông ABCD. E, F, I theo thứ tự là trung điểm của BC, CD, DA. H, K theo thứ tự là giao điểm của IB, DE với AF. CMR:a) AH=HKb) IB vuông góc với AFc)...

1

NL

Nguyễn Lê Phước Thịnh

17 tháng 10 2022

Bài 3:

a: Xét ΔCDF vuông tại C và ΔBCE vuông tại B có

CD=BC

CF=BE

Do đó: ΔCDF=ΔBCE
=>góc CDF=góc BCE

=>góc BCE+góc MFC=góc DFC+góc CDF=90 độ

=>CE vuông góc với DF

b: Gọi Klà trung điểm của CD và N là giao của AK và DF

Xét tứ giác AECK có

AE//CK

AE=CK

Do dó: AECK là hình bình hành

SUy ra: AK=CE và AK//CE

=>AK vuông góc với DF

Xét ΔDMC có

K là trung điểm của DC

KN//MC

Do đó: N là trung điểm của DM

Xét ΔAMD có

AN vừa là đường cao, vừa là đường trung tuyến

nên ΔAMD cân tại A

P

Persmile

28 tháng 11 2021

Cho hình vuông ABCD, gọi E, Ftheo thứ tự là trung điểm của AB, BC. CE cắt DF ở I
a) C/m: CE = DF và CE vuông góc DF
b) Kẻ AH vuông góc DF, AH cắt CD ở K. C/m: KD = KC
c) Gọi G là trung điểm AD, BG cắt AH ở M và cắt CE tại N. C/m: MNIH là hình vuông
d) C/m: AI = AB

0

A

anhmiing

28 tháng 11 2019 - olm

bài 1:cho tứ giác ABCD có 2 đường chéo ac và bd vuông góc với nhau . gọi m,n,p,q lần lượt là tđ của các cạnh ab,bc,cd,daa) mnpq là hình j?b)mnpq là hình vuôn thì abcd cần đk j?c)cho ac=6cm,bd=8cm. tính diện tích mnpqbài 2: Cho abc vuông tại a . lấy d thuộc cạnh bc, e là tđ của ac, f đối xứng với d qua e . cm afcd là hbhbài 3: cho hình thoi abcd . gọi o là giao của 2 đường chéo . qua b vẽ đường thẳng song song...

1

AC

ĂN CỨT CHÓ

28 tháng 11 2019

76276712

A

anhmiing

28 tháng 11 2019 - olm

bài 1:cho tứ giác ABCD có 2 đường chéo ac và bd vuông góc với nhau . gọi m,n,p,q lần lượt là tđ của các cạnh ab,bc,cd,daa) mnpq là hình j?b)mnpq là hình vuôn thì abcd cần đk j?c)cho ac=6cm,bd=8cm. tính diện tích mnpqbài 2: Cho abc vuông tại a . lấy d thuộc cạnh bc, e là tđ của ac, f đối xứng với d qua e . cm afcd là hbhbài 3: cho hình thoi abcd . gọi o là giao của 2 đường chéo . qua b vẽ đường thẳng song song...

0

NT

Nguyễn Tuấn

15 tháng 2 2016 - olm

Bài 9: Cho hình bình hành ABCD có BC = 2 AB và A = 600. Gọi M, N lần lượt trung điểm củaBC và AD. E là điểm đối xứng với A qua B.a.Tứ giác ABMN là hình gì? Vì sao?b.Chứng minh tứ giác AEMN là hình thang cân.Bài 10: Cho ba tia Ox, Oy, Oz tạo thành góc xOy = góc yOz=600. Một đường thẳng cắt ba tia đó lần lượt tại A, B, C. Qua B kẻ BB’ songsong với Oz(B’ thuộc Ox). Chứng minhTam giác OBB’ đềuBài 11 : Cho tam...

0

VT

Vũ Thùy Linh

12 tháng 11 2015 - olm

Bài 1: Cho hình vuông ABCD, M thuộc AB, N là trung điểm DM trên BC lấy E sao cho BE=BM gọi I là trung điểm AB CMR AE vuông góc NIBài 2 cho tam gicá ABC vuông tại A và hình vuông BCDECMR AB+AC nhỏ hơn Hoặc bằng CEBài 3: cho điểm M nằm trên đoạn thẳng AB. Vẽ về một phía của AB các hình vuông AMCD và BMEFa) CMR: AE=BC; AE vuông góc với BCBài 4: CHO hình vuông ABCD, gọi d là đường thằng bất kì đi qua giao điểm O của...

0

Y

ytr

14 tháng 11 2019

Bài 1 : Cho hình vuông ABCD có E ,F là TĐ AB ,AC

a) CM: CE vuông với DF

b) Gọi DF cắt CE tại M . CM AM = AB

Bài 2:Cho hình vuông ABCD . Qua M thuộc đường chéo AC , Kẻ ME vuông với AD ; MF vuông CD . CMR:

a) BE vuông với AF

b) BM vuông với EF

1

Y

ytr

14 tháng 11 2019

c) BM , AF , CE đồng quy

HV

Hoa Vô Khuyết

18 tháng 8 2023

Bài 1: Cho hình bình hành ABCD có đường chéo lớn AC,tia Dx cắt SC, AB, BC lần lượt tại I, M, N. Vẽ CE vuông góc với AB, CF vuông góc với AD, BG vuông góc với AC. Gọi K là điểm đối xứng với D qua I. Chứng minh rằnga) IM. IN = ID2b)\(\dfrac{\text{KM}}{\text{KN }}\)= \(\dfrac{\text{DM}}{\text{DN}}\)c) AB. AE + AD. AF = AC2(VẼ CẢ...

0

Y

ytr

14 tháng 11 2019

Bài 1 : Cho hình vuông ABCD có E ,F là TĐ AB ,AC

a) CM: CE vuông với DF

b) Gọi DF cắt CE tại M . CM AM = AB

Bài 2:Cho hình vuông ABCD . Qua M thuộc đường chéo AC , Kẻ ME vuông với AD ; MF vuông CD . CMR:

a) BE vuông với AF

b) BM vuông với EF

c) BM , AF , CE đồng quy

1

VM

Vũ Minh Tuấn

15 tháng 11 2019

Nguồn: loigiaihay.com

Bài 1:

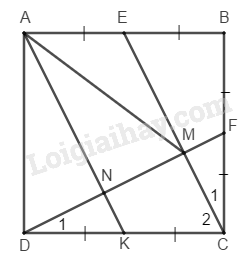
Mà \(AD=AB\) (vì \(ABCD\) là hình vuông).

=> \(AM=AB\left(đpcm\right).\)

Chúc bạn học tốt!