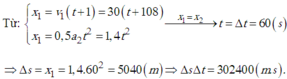Một ôtô chạy đều trên một con đường thẳng với tốc độ 25m/s (vượt quá tốc độ) thì bị cảnh sát giao thông phát hiện. Chỉ sau 2s khi ôtô đi qua một cảnh sát, anh cảnh sát này bắt đầu đuổi theo với gia tố...

BL

Bùi Linh Nhi

20 tháng 10 2019

Một ôtô chạy đều trên một con đường thẳng với tốc độ 25m/s (vượt quá tốc độ) thì bị cảnh sát giao thông phát hiện. Chỉ sau 2s khi ôtô đi qua một cảnh sát, anh cảnh sát này bắt đầu đuổi theo với gia tốc không đổi và bằng 6m/s2. Thời điểm và vị trí anh cảnh sát đuổi kịp ôtô...

Đọc tiếp

#Vật lý lớp 10

0

PT

Phú Tuyên Nguyễn

31 tháng 8 2023

Một ôtô chạy đều trên một con đường thẳng với tốc độ 25m/s (vượt quá tốc độ) thì bị cảnh sát giao thông phát hiện. Chỉ sau 2s khi ôtô đi qua một cảnh sát, anh cảnh sát này bắt đầu đuổi theo với gia tốc không đổi và bằng 6m/s2. Thời điểm và vị trí anh cảnh sát đuổi kịp ôtô làA.sau 1s kể từ lức anh cảnh sát xuất phát, cách vị trí xuất phát của anh cảnh sát 75m.B. sau 10s kể từ lúc anh cảnh sát...

Đọc tiếp

#Vật lý lớp 10

1

M

meme

2 tháng 9 2023

Để giải bài toán này, ta sử dụng các công thức về vận tốc, thời gian và quãng đường đi được.

Cho ô tô chạy với vận tốc ban đầu v0 = 25 m/s và cảnh sát có gia tốc a = 6 m/s^2.

Ta có công thức vận tốc: v = v0 + at

Với v là vận tốc tại thời điểm t, v0 là vận tốc ban đầu, a là gia tốc và t là thời gian.

Ta xác định thời điểm và vị trí anh cảnh sát đuổi kịp ô tô.

Để anh cảnh sát đuổi kịp ô tô, ta giải phương trình sau để tìm thời gian cần thiết: 25 + 6t = 0 (vận tốc ô tô) và 6t = 75 (quãng đường cảnh sát cần phải bắt kịp ô tô)

Ta giải phương trình 6t = 75 để tìm thời gian cần thiết: 6t = 75 t = 75/6 t ≈ 12.5 giây

Vậy sau khoảng 12.5 giây, anh cảnh sát sẽ đuổi kịp ô tô và cách vị trí xuất phát của anh cảnh sát là 75m.

Ta xác định thời điểm và vị trí anh cảnh sát đuổi kịp ô tô.

Ta giải phương trình sau để tìm thời gian cần thiết: 25 + 6t = 0 (vận tốc ô tô) và 6t = 300 (quãng đường cảnh sát cần phải bắt kịp ô tô)

Ta giải phương trình 6t = 300 để tìm thời gian cần thiết: 6t = 300 t = 300/6 t = 50 giây

Vậy sau khoảng 50 giây, anh cảnh sát sẽ đuổi kịp ô tô và cách vị trí xuất phát của anh cảnh sát là 300m.

Do đó, đáp án là C. Sau 12s kể từ lúc anh cảnh sát xuất phát, cách vị trí xuất phát của anh cảnh sát 300m.

Đúng(0)

HD

Hoàng Đức Long

15 tháng 1 2019

Một ô tô chạy đều trên đường thẳng với tốc độ 30 m/s vượt quá tốc độ cho phép và bị cảnh sát giao thông phát hiện. Chỉ sau 108s khi ô tô đi ngang qua một cảnh sát, anh này phóng xe đuổi theo với gia tốc có độ lớn bằng 2,8 m/s2. Sau thời gian ∆ t thì anh cảnh sát đuổi kịp ô tô và quãng đường anh đi được là ∆ s.Độ lớn của ∆ s ∆ t gần giá trị nào...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

15 tháng 1 2019

Chọn A

Đúng(0)

HD

Hoàng Đức Long

27 tháng 8 2018

Một ô tô chạy đều trên đường thẳng với tốc độ 30 m/s vượt quá tốc độ cho phép và bị cảnh sát giao thông phát hiện. Chỉ sau 108s khi ô tô đi ngang qua một cảnh sát, anh này phóng xe đuổi theo với gia tốc có độ lớn bằng 2,8 m/s2. Sau thời gian △ t thì anh cảnh sát đuổi kịp ô tô và quãng đường anh đi được là △ s . Độ lớn của △ s △ t gần giá...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

27 tháng 8 2018

Đúng(0)

TT

Thái Thị Thiên Thu

25 tháng 7 2016

Một ô tô chạy đều trên đường thẳng với vận tốc là 30 m/s vượt quá tốc độ cho phép và bị cảnh sát giao thông phát hiện. Chỉ sau 1s khi ô tô đi ngang qua 1 cảnh sát, cảnh xát phóng xe đuổi theo với gia tốc không đổi 3 m/s²

a) Sau bao lâu cảnh sát đuổi kịp ô tô

b) Quãng đường anh di được là bn?

#Vật lý lớp 10

2

LN

Lê Nguyên Hạo

25 tháng 7 2016

Chọn tọa độ và vị trị của anh cảnh sát:

Ta có :

Phương trình chuyển động của xe ô tô là :

x₁ = 30 + 30t

Phương trình chuyển động của anh cảnh sát :

x₂ = $\frac{3t^2}{2}$

Khi gặp nhau thì x₁ = x₂

<=> 30 + 30t = $\frac{3t^2}{2}$

t = 21 (giây)

S = 1,5t²=658,6 (m)

Vậy sau 21 giây cảnh sát đuổi kịp ô tô

Quãng đường anh đi được là 658,6 m

Đúng(1)

NV

Nguyễn Văn Dũng

4 tháng 8 2016

khó quá

Đúng(0)

NP

Nguyen Phuong

30 tháng 9 2016

LÀM GIÚP MÌNH! MÌNH CẦN GẤP!!B1: Xe thứ nhất chuyển động nhanh dần đều vs gia tốc 0,25 m/s2 , đúng lúc đó một xe thứ 2 chuyển động thẳng đều vs vận tốc 36 m/s vượt qua nó. Hởi xe thứ nhất đuổi kịp xe thứ 2 thì quãng đường và vận tốc là bao nhiêu?B2: Một ô tô chạy đều trên 1 con đường thẳng vs vận tốc 30m/s vượt qua tốc độ cho phép và bị cảnh sát giao thông phát hiện. Chỉ sau...

Đọc tiếp

#Vật lý lớp 10

2

KA

Kiều Anh

19 tháng 9 2017

B1 Phương trình chuyển động của xe thứ nhất là:

X1=x0+v1.t+1/2.a.t²=1/2.0,25.t²=0,125.t²

Phương trình chuyển động của xe thứ hai là:

X2=xo+v.t=36.t

2 xe gặp nhau khi X1=X2 hay 0,125.t²=36.t

=>t=288(s)

X1=10369m

v=v0+a.t=0+0,25.288=72(m/s)

Đúng(0)

NP

Nguyen Phuong

30 tháng 9 2016

a. Các bn chỉ cần trả lời giúp mình b1 là được rồi. Thanks

Đúng(0)

VL

Vũ Lan Phương

8 tháng 8 2016

Trên đường có một dãy dài ô tô chuyển động đều.Khoảng cách giữa hai ô tô liền nhau là như nhau.Một xe cảnh sát giao thông đi xe moto theo hướng của đoàn xe thì phát hiện ra: nếu anh ta cho xe chạy với vận tốc v1=36km/h thì cứ sau t1=10s thì có 1 xe trong đoàn vượt qua anh ta,còn đi với v2=90km/h thì cứ t2=20s thi anh ta lại vượt một xe trong hàng.Khi xe cảnh sát đi ngược chiều với đoàn xe với v3...

Đọc tiếp

#Vật lý lớp 8

2

PQ

pham quan

28 tháng 8 2016

45km

Đúng(0)

NT

Nguyễn Thị Diễm Quỳnh

13 tháng 8 2017

v3=0

Đúng(1)

EN

Emilia Nguyen

15 tháng 9 2019

Một oto chạy đều trên đường thẳng với vận tốc 30m/s vượt quá tốc độ qui định và bị cảnh sát giao thông phát hiện, chỉ sau 1s sau khi ô tô chạy ngang, cảnh sát phóng xe chạy theo với gia tốc không đổi 3m/s2. HỎi sau bao lâu cảnh sát đuổi kịp ô tô

#Vật lý lớp 10

1

DH

Diệu Huyền

15 tháng 9 2019

Tham khảo:

Chọn tọa độ và vị trị của anh cảnh sát:

Ta có :

Phương trình chuyển động của xe ô tô là :

x1 = 30 + 30t

Phương trình chuyển động của anh cảnh sát :

x₂=$\frac{3t^2}{2}$

Phương trình chuyển động của anh cảnh sát :

x₂=$\frac{3t^2}{2}^{ }$

Khi gặp nhau thì x1 = x2

<=> 30 + 30t = $\frac{3t^2}{2}$

t = 21 (giây)

S = 1,5t^2 =658,6 (m)

Vậy sau 21 giây cảnh sát đuổi kịp ô tô

Quãng đường anh đi được là 658,6 m

Đúng(0)

LN

le nguyen bao tran

3 tháng 10 2018

một ô tô chạy đều trên đường thẳng với vận tốc 30m/s vượt quá tốc độ cho phép . chỉ sau 1s khi ô tô đi ngang qua một anh cảnh sát giao thông , anh này phóng xe đuổi theo với gia tốc không đổi 3m/s2 â) hỏi sau bao lâu thì anh cảnh sát đuổi kịp ô tô b) quãng đường anh cảnh sát đi được là bao...

Đọc tiếp

#Vật lý lớp 10

1

TS

Thời Sênh

3 tháng 10 2018

chọn gốc toạ độ là vị trí của anh cảnh sát
ta có :
phương trình chuyển động của xe ô tô $x 1 =30+30t$
phương trình chuyển động của anh cảnh sát $x2=3t 2 /2$
Khi hai xe gặp nhau $x1=x2$
<=> 30 + 30t = $3t 2 /2$
=> t = 21 s
S = $1,5t 2$ = 658.6 (m )

Đúng(0)

TN

Trần Nguyễn Ngọc

3 tháng 8 2016

Một ô tô chạy đều trên một con đường thẳng với $v=30$m/s (vượt quá tốc độ cho phép) và bị cảnh sát giao thông phát hiện. Chỉ sau 1(s) khi ô tô đi qua cảnh sát, anh này phóng xe đuổi theo với gia tốc không đổi bằng 3(m/s2) . Tính thời gian và quãng đường mà anh cảnh sát đuổi kịp ô...

Đọc tiếp

#Vật lý lớp 8

3

VD

Võ Đông Anh Tuấn

3 tháng 8 2016

Chọn gốc toạ độ là vị trí của anh cảnh sát
Ta có :
Phương trình chuyển động của xe ô tô $x_1=30+30t$

Phương trình chuyển động của anh cảnh sát $x_2=\frac{3t^2}{2}$

Khi hai xe gặp nhau $x_1=x_2$

$\Leftrightarrow30+30t=\frac{3t^2}{2}$

$\Rightarrow t=21\left(s\right)$

$S=1,5t^2=661,5\left(m\right)$

Đúng(0)

NB

Nhók Bướq Bỉnh

3 tháng 8 2016

Chọn trục tọa độ trùng với đường đi, gốc tọa độ trùng với vị trí của anh cảnh sát giao thông, gốc thời gian là lúc anh xuất phát. Khi đó ô tô đã ở vị trí cách anh cảnh sát  30m. Phương trình chuyển động của ô tô và của anh cảnh sát lần lượt là:
                       x1=30+30t (1)
                       x2=$\frac{3t}{2}$ ²( 2)
Khi anh cảnh sát đuổi kịp thì  x1=x2. Ta có:
                       30+30t=$\frac{3t}{2}$ ², hay là:
                       1,5t²−30t−30=0(3)
Giải phương trình này, ta được

t1=20,95s và t2=−0,95s

. Vậy, sau 21s anh cảnh sát đuổi kịp ô tô.

Thay t=21s vào (1) hoặc (2) ta tìm được quãng đường đi được.
Kết quả là: s=661m.

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP