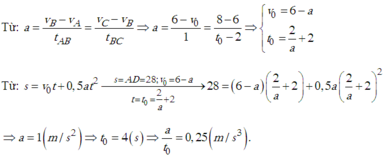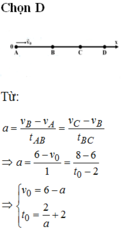Một xe máy chuyển động thẳng nhanh dần đều trên đoạn AD dài 28m. Sau khi xe qua A được 1s xe tới B với vận tốc 6m/s. 1s trước khi tới D, xe ở C và vận tốc 8m/s. Thời gian xe đi trên đoạn đường AD là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DC
25 tháng 9 2019
Phân tích bài toán
SAD=28m; gọi t là khoảng thời gian chất điểm đi hết đoạn đường AD
Tại B cách A 1 giây:
vB=vo + a.1=6 => vo=6-a (1)
Tại điểm C cách điểm D 1 giây:
vC=vo + a(t-1)=8 => vo + at – a=8 (2)
Giải
từ (1) và (2) => t=2a+22a+2 (3)
SAD=vot + 0,5at2=28 (4)
thay (1); (3) vào (4)
=> a=1m/s2 => t=4s;
SCD=vC.1 + 0,5a.12=8,5m.
MD
25 tháng 9 2019
Phân tích bài toán
SAD=28m; gọi t là khoảng thời gian chất điểm đi hết đoạn đường AD
Tại B cách A 1 giây:
vB=v0 + a.1=6 => v0=6-a (1)
Tại điểm C cách điểm D 1 giây:
vC=v0 + a(t-1)=8 => v0 + at – a=8 (2)
Giải
từ (1) và (2) => t=2a+22a+2 (3)
SAD=v0t + 0,5at2=28 (4)
thay (1); (3) vào (4)
=> a=1m/s2 => t=4s;
SCD=vC.1 + 0,5a.12=8,5m.
SAD=28m; gọi t là khoảng thời gian chất điểm đi hết đoạn đường AD
Tại B cách A 1 giây:
vB=v0 + a.1=6 => v0=6-a (1)
Tại điểm C cách điểm D 1 giây:
vC=v0 + a(t-1)=8 => v0 + at – a=8 (2)
Giải
từ (1) và (2) => t=2a+22a+2 (3)
SAD=v0t + 0,5at2=28 (4)
thay (1); (3) vào (4)
=> a=1m/s2 => t=4s;
SCD=vC.1 + 0,5a.12=8,5m.
2 tháng 12 2021
Lần sau nếu đăng 2 bài bạn tách ra nhé cho dễ nhìn.
Bài 2.
Tóm tắt: \(v_0=18\)km/h=5m/s
\(a=0,5\)m/s2
\(S=24m\)
\(v=?\)
Bài giải:
Vận tốc xe sau: \(v^2-v^2_0=2aS\)
\(\Rightarrow v=\sqrt{2aS+v^2_0}=\sqrt{2\cdot0,5\cdot24+5^2}=7\)m/s
2 tháng 12 2021
Bài 1.
Gia tốc vật:
\(a=\dfrac{v^2-v^2_0}{2S}=\dfrac{2^2-0}{2\cdot16}=0,125\)m/s2
TK
23 tháng 9 2021
Quãng đường đi được trong 1s cuối
\(\dfrac{1}{2}\cdot a\cdot5^2-\dfrac{1}{2}\cdot a\cdot\left(5-1\right)^2=1,5\Rightarrow a=\dfrac{1}{3}\left(\dfrac{m}{s^2}\right)\)
Vậy gia tốc của vật là 1/3 (m/s^2)
Quãng đường đi dc từ khi hãm phanh đến khi dừng lại
\(s=\dfrac{1}{2}\cdot\dfrac{1}{3}\cdot5^2=\dfrac{25}{6}\left(m\right)\)
<chỗ nào sai chỉ mình hoặc ko hiểu thì bình luận câu trả lời nha>
23 tháng 9 2021
\(v^2-v^2_0=2as\)
\(\Rightarrow5^2-v^2_0=2a.10\)
\(\Rightarrow25-v^2_0=20a\left(1\right)\)
Lại có: \(10^2-v^2_0=2a.47,5\)
\(\Rightarrow100-^2_0=95a\left(2\right)\)
Từ (1) và (2) ta có hệ : \(\left\{{}\begin{matrix}25-v^2_0=20a\\100-v^2_0=95a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=1m\text{/ }s^2\\v_0=\sqrt{5m\text{/ }s}\end{matrix}\right.\)
TK
26 tháng 9 2021
Đổi 54km/h=15m/s
Chiều dài của dốc là
\(s=\dfrac{v^2-v_0^2}{2a}=\dfrac{15^2-3^2}{2\cdot0,2}=540\left(m\right)\)
Thời gian xuống dốc :
\(t=\dfrac{v-v_0}{a}=\dfrac{15-3}{0,2}=60\left(s\right)\)
