giúp dùm câu 3 vs ạ 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
YL
7
KK
7 tháng 9 2021
a. -2x(x3 - 3x2 - x + 1)
= -2x4 + 6x3 + 2x2 - 2x
c. 3x2(2x3 - x + 5)
= 6x5 - 3x3 + 15x2
7 tháng 9 2021
Bài 3:
a: Ta có: \(6x\left(5x-3\right)+3x\left(1-10x\right)=7\)
\(\Leftrightarrow30x^2-18x+3x-30x^2=7\)
\(\Leftrightarrow x=-\dfrac{7}{15}\)
b: Ta có: \(3x\left(12x-4\right)-9x\left(4x-3\right)=30\)
\(\Leftrightarrow36x^2-12x-36x^2+27x=30\)
hay x=2
c: ta có: \(x\left(5-2x\right)-2x\cdot\left(x-1\right)=15\)
\(\Leftrightarrow5x-2x^2-2x^2+2x-15=0\)
\(\Leftrightarrow-4x^2+7x-15=0\)
\(\text{Δ}=7^2-4\cdot\left(-4\right)\cdot\left(-15\right)=-191\)
Vì Δ<0 nên phương trình vô nghiệm
10 tháng 8 2021
Em ơi khi đăng bài em đăng 1-2 bài cho một lượt hỏi thui nha!
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
làm dùm tớ câu c vs ạ
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
26 tháng 11 2021
a) Số nguyên tử Al trong 1 mol nguyên tử Al: 6.1023 (nguyên tử)
b) Số phân tử O2 có chứa 1 phân tử O2 là: 6.1023 (phân tử)
c) Số phân tử CO2 trong 0,5 mol phân tử khí CO2 : 6.1023.0,5=3.1023 (phân tử)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 3 2021
11. \(I=\int\limits^2_1x\sqrt{x^2+1}dx\)
Đặt \(\sqrt{x^2+1}=t\Leftrightarrow x^2=t^2-1\Rightarrow xdx=tdt\) ; \(\left\{{}\begin{matrix}x=1\Rightarrow t=\sqrt{2}\\x=2\Rightarrow t=\sqrt{5}\end{matrix}\right.\)
\(I=\int\limits^{\sqrt{5}}_{\sqrt{2}}t.tdt=\int\limits^{\sqrt{5}}_{\sqrt{2}}t^2dt=\dfrac{1}{3}t^3|^{\sqrt{5}}_{\sqrt{2}}=\dfrac{1}{3}\left(5\sqrt{5}-2\sqrt{2}\right)\)
12. Đặt \(\sqrt[3]{8-4x}=t\Rightarrow x=\dfrac{8-t^3}{4}\Rightarrow dx=-\dfrac{3}{4}t^2dt\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow t=2\\x=2\Rightarrow t=0\end{matrix}\right.\)
\(I=\int\limits^0_2t.\left(-\dfrac{3}{4}t^2dt\right)=\dfrac{3}{4}\int\limits^2_0t^3dt=\dfrac{3}{16}t^4|^2_0=3\)
13. Đặt \(\sqrt{3-2x}=t\Rightarrow x=\dfrac{3-t^2}{2}\Rightarrow dx=-tdt\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow t=\sqrt{3}\\x=1\Rightarrow t=1\end{matrix}\right.\)
\(I=\int\limits^1_{\sqrt{3}}\dfrac{-tdt}{t}=\int\limits^{\sqrt{3}}_1dt=t|^{\sqrt{3}}_1=\sqrt{3}-1\)
MT
2
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
1.
\(y'=x^2-6x+5=0\Rightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
Dấu của y' trên trục số:
Hàm đồng biến trên các khoảng \(\left(-\infty;1\right)\) và \(\left(5;+\infty\right)\)
Hàm nghịch biến trên \(\left(1;5\right)\)
3.
TXĐ: \(D=R\backslash\left\{2\right\}\)
\(y'=\dfrac{-5}{\left(x-2\right)^2}< 0;\forall x\in D\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;2\right)\) và \(\left(2;+\infty\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
4.
\(y'=4x^3+4x=4x\left(x^2+1\right)=0\Rightarrow x=0\)
Dấu của y':
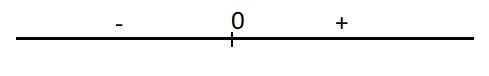
Hàm đồng biến trên \(\left(0;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;0\right)\)
6.
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-1;1\right)\)
TH
Giúp dùm mik câu b với ạ!! Vẽ hình câu b giúp mik luôn nhé
1
21 tháng 6 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>AD=ED
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc EBF chung
=>ΔBEF=ΔBAC
=>BF=BC
2BF=BF+BC>FC
Bạn tự làm tóm tắt + vẽ hình nhé!
a. Điện trở của R23: \(R_{23}=\dfrac{R2.R3}{R2+R3}=\dfrac{24.24}{24+24}=12\Omega\)
Điện trở nối tiếp: \(R_{123}=R_1+R_{23}=12+12=24\Omega\)
Cường độ dòng điện toàn mạch: \(I=\dfrac{U}{R}=\dfrac{12}{24}=0,5A\)
b. Điện trở của R12: \(R_{12}=R1+R2=12+24=36\Omega\)
Điện trở tương đương: \(R=\dfrac{R12.R3}{R12+R3}=\dfrac{36.24}{36+24}=14,4\Omega\)
\(U=U_{12}=U_3=12V\)(R12//R3)
Cường độ dòng điện của toàn mạch và R3:
\(I=\dfrac{U}{R}=\dfrac{12}{14,4}=\dfrac{5}{6}A\)
\(I_3=\dfrac{U3}{R3}=\dfrac{12}{24}=0,5A\)
Do R12//R3 nên I12 = I - I3 = \(\dfrac{5}{6}-0,5=\dfrac{1}{3}A\)
Do R1 nt R2 nên I12 = I1 = I2 = 1/3A
Hiệu điện thế giữa 2 đầu R1: \(U1=R1.I1=12.\dfrac{1}{3}=4V\)