Hai chất điểm A và B chuyển động tròn đều lần lượt trên hai đường tròn có bán kính khác nhau, nhưng có cùng gia tốc. Biết rằng tốc độ quay của chất điểm A gấp đôi tốc độ quay của chất điểm B. Vậy bán kính quỹ đạo của A bằng bao nhiêu lần bán kính quỹ đạo của chất điểm B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án A
+ Chuyển động tròn đều có tốc độ góc ω không đổI
+ Ta có ![]()
![]()
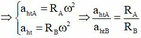
=20/15=4/3

Chọn A.
Quỹ đạo của điểm A và B có án kính lần lượt là: rA = 20 cm, rB = 20 – 5 = 15 cm.
Hai điểm A, B có cùng tốc độ quay
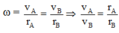
Tỉ số gia tốc:
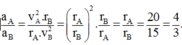

Chọn A.
Quỹ đạo của điểm A và B có án kính lần lượt là: r A = 20 cm, r B = 20 – 5 = 15 cm.
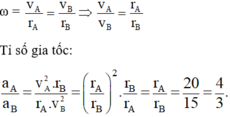

R=50cm=0,5m
Ta có:T=\(\dfrac{2\pi}{\omega}\)=\(\dfrac{2\pi}{2}\)=\(\pi\)
Ta có:\(\nu\)=r.\(\omega\)=0,5.2=1(m/s)

Chọn A.
Góc quét được sau thời gian t: φ = ω t ⇒ φ M = 10 π t φ N = 5 π t
Hai chất điểm gặp nhau khi hiệu góc quét bằng một số nguyên lần 2 π tức là: k 2 π = φ M - φ N = 5 π t ⇒ t = 0 , 4 k ( s ) ( k = 1 ; 2 ; . . . )
Gặp nhau lần 3 ứng với k = 3 => t1 = 1,2(s)
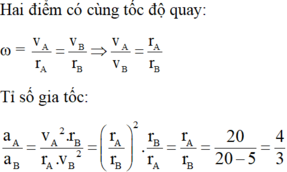
\(\frac{vA}{vB}\)=\(\frac{aht.rA}{aht.rB}\)=\(\frac{rA}{rB}\)=4➜rA=4rB