cho hình chóp S.ABC, biết tam giác sab vuông tại đỉnh S và có AB= 3 cm, SA=1cm. Tam giác sbc vuông tại đỉnh S vf có AC =4cm
1 chứng minh AS vuông góc với mặt phẳng SBC
2 tính diện tích xung quanh của hình chóp
3 tính thể tích của hình chóp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 2 2018
Đáp án D
Gọi H là trung điểm của BC ta có: A H ⊥ B C Do A B C ⊥ S B C ⇒ A H ⊥ S B C
Đặt A H = x ⇒ H C = a 2 − x 2 = H B = S H ⇒ Δ S B C
vuông tại S (do đường trùng tuyến bằng cạnh đối diện). Suy ra B C = S B 2 + S C 2 = a 3 . Gọi O là tâm đường tròn ngoại tiếp Δ A B C ⇒ O ∈ A H ⇒ O A = O B = O C = OS .Ta có: R = R A B C = A C 2 sin B , trong đó sin B = A H A B = A S 2 − S H 2 A B = 1 2 Do đó R C = a ⇒ S x q = 4 π R 2 C = 4 π a 2 .
CM
1 tháng 8 2017
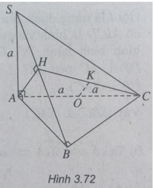
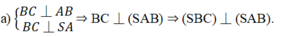
b) AH ⊥ SB mà SB là giao tuyến của hai mặt phẳng vuông góc là (SBC) và (SAB) nên AH ⊥ (SBC).
c) Xét tam giác vuông SAB với đường cao AH ta có:
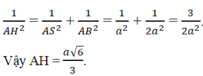
d) Vì OK ⊥ (SBC) mà AH ⊥ (SBC) nên OK // AH, ta có K thuộc CH.
OK = AH/2 = (a√6)/6.