Tìm m để phép chia A(x) = 2x2 - x + m chia B(x) = 2x - 5 có dư =-10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
10 tháng 4 2018
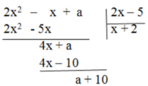
A(x) chia cho B(x) có số dư bằng -10 ⇒ a + 10 = -10 ⇒ a = -20
1 tháng 9 2021
b: Ta có: f(x):g(x)
\(=\dfrac{x^3-2x^2+3x+a}{x+1}\)
\(=\dfrac{x^3+x^2-3x^2-3x+6x+6+a-6}{x+1}\)
\(=x^2-3x+6+\dfrac{a-6}{x+1}\)
Để f(x):g(x) là phép chia hết thì a-6=0
hay a=6
1 tháng 9 2021
d: Ta có: f(x):g(x)
\(=\dfrac{x^3-2x^2+3x+5}{x+1}\)
\(=\dfrac{x^3+x^2-3x^2-3x+6x+6-1}{x+1}\)
\(=x^2-3x+6+\dfrac{-1}{x+1}\)
Để f(x) chia hết cho g(x) thì \(x+1\in\left\{1;-1\right\}\)
hay \(x\in\left\{0;-2\right\}\)
30 tháng 8 2021
a: Thay a=3 vào f(x), ta được:
\(f\left(x\right)=x^3-2x^2+3x+3\)
\(\dfrac{f\left(x\right)}{g\left(x\right)}=\dfrac{x^3-2x^2+3x+3}{x+1}\)
\(=\dfrac{x^3+x^2-3x^2-3x+6x+6-3}{x+1}\)
\(=x^2-3x+6-\dfrac{3}{x+1}\)
NH
0
29 tháng 10 2021
Bài 1:
Ta có: \(5x^3-3x^2+2x+a⋮x+1\)
\(\Leftrightarrow5x^3+5x^2-8x^2-8x+10x+10+a-10⋮x+1\)
\(\Leftrightarrow a-10=0\)
hay a=10
3 tháng 1 2022
a: \(\dfrac{A}{B}=\dfrac{6x^3+3x^2-10x^2-5x+4x+2+m-2}{2x+1}=3x^2-5x+2+\dfrac{m-2}{2x+1}\)
b: Để A chia B dư 4 thì m-2=4
hay m=6
2x^2-x+m 2x-5 x+2 2x^2-5x - 4x+m 4x-10 - m+10
Vì \(A\left(x\right):B\left(x\right)\)dư -10 \(\Leftrightarrow m+10=-10\)
Vậy ...
\(\Leftrightarrow m=0\)